8. Sınıf Matematik Ders Kitabı Sayfa 105-106-107-108-109. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 105-106-107-108-109. Cevapları MEB Yayınları bölümünde, ders kitabı sayfa 105-106-107-108-109 konularına ait cevapları bulabilirsiniz. “2. Ünite Değerlendirme Soruları Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 105-106-107-108-109. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
2. Ünite Değerlendirme Soruları Cevapları
2. Ünite: Tam kare sayılar, bir sayının karekökü alınarak bulunan ve doğal sayı olan değerlerdir. Köklü ifadelerde ise basitleştirme ve birim çevirileri yaparken dikkatli olunmalıdır.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 105 Cevapları MEB Yayınları
1. En küçük üç basamaklı tam kare doğal sayı ile en büyük iki basamaklı tam kare doğal sayının farkı kaçtır?
Cevap:
Üç basamaklı en küçük tam kare: 100 (çünkü 10² = 100 ve 100 üç basamaklı ilk tam karedir).
İki basamaklı en büyük tam kare: 81 (çünkü 9² = 81 ve 81 iki basamaklı en büyük tam karedir).
Fark: 100 − 81 = 19.
Sonuç: B) 19.
2. 1, 6 ve 9 rakamlarını kullanarak oluşturulabilecek üç basamaklı tam kare doğal sayıların toplamı kaçtır?
Cevap:
Bu rakamlarla oluşabilecek üç basamaklı permütasyonlar: 169, 196, 619, 691, 916, 961.
Her birini kontrol edelim:
169 = 13² ⇒ tam karedir.
196 = 14² ⇒ tam karedir.
619 ≠ tam kare (24² = 576, 25² = 625 → 619 arada).
691 ≠ tam kare (26² = 676, 27² = 729 → 691 arada).
916 ≠ tam kare (30² = 900, 31² = 961 → 916 arada).
961 = 31² ⇒ tam karedir.
Tam kare olanlar: 169, 196, 961.
Toplam = 169 + 196 + 961 = 1326.
Sonuç: D) 1326.
3.
a ve b pozitif tam sayı, √a ile √b arasında sadece 3 doğal sayısı bulunmaktadır.
Buna göre √(a + b) ifadesinin alabileceği en küçük değer hangi doğal sayıya daha yakındır?
Cevap:
“a ile b arasında sadece 3 doğal sayı” demek: aradaki doğal sayı sayısı = 3. Bu durum, b − a − 1 = 3 ⇒ b − a = 4.
Pozitif en küçük a için a = 1 alınırsa b = a + 4 = 5 olur (başka daha küçük a olamaz çünkü a pozitif tam sayı olmalı).
İstenen ifade: √a + √b = √1 + √5 = 1 + √5.
√5 ≈ 2,2360679… (bilinen değer).
1 + √5 ≈ 1 + 2,236 = 3,236…
En yakın doğal sayı: 3 (çünkü 3,236 en yakın tam sayıya yuvarlanınca 3 olur).
Sonuç: B) 3.
4.
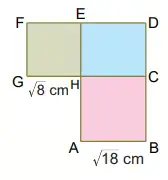
Yandaki şekilde ABCH ve GHEF birer karedir.
|AB| = √18 cm, |GH| = √8 cm ise bu şeklin çevresi kaç santimetredir?
Cevap:
ABCH (pembe) bir kare ve kenarı s_b = √18 = 3√2 cm
GHEF (yeşil) bir kare ve kenarı s_g = √8 = 2√2 cm
Şekilde ayrıca mavi bir kare daha bulunmaktadır ve bu karenin de kenarı s_b = √18 = 3√2 cm’dir
Her karenin ayrı ayrı çevreleri:
Pembe karenin çevresi = 4 × s_b = 4 × 3√2 = 12√2 cm
Mavi karenin çevresi = 4 × s_b = 4 × 3√2 = 12√2 cm
Yeşil karenin çevresi = 4 × s_g = 4 × 2√2 = 8√2 cm
Ayrı ayrı toplam çevre (ayrık kareler halinde) = 12√2 + 12√2 + 8√2 = 32√2 cm
Ancak şekilde iki ortak kenar vardır:
Mavi ile pembe kare arasında bir ortak kenar (uzunluk s_b = 3√2 cm)
Mavi ile yeşil kare arasında bir ortak kenar (uzunluk s_g = 2√2 cm)
Bu ortak kenarlar dış çevreye dahil olmaz, ayrı ayrı sayıldığında iki kere sayılmıştır. Bu yüzden toplamdan bu kenarların iki katını çıkarmalıyız:
Dış çevre = 32√2 – 2×(3√2) – 2×(2√2) = 32√2 – 6√2 – 4√2 = 22√2 cm
Sonuç: 22√2 cm (yaklaşık 31,11 cm)
5.
I. √144 + 25
II. √144 – 25
III. √144 ÷ 25
IV. √144 . 25
Yukarıdaki karekök ifadelerden hangileri rasyonel sayıya eşittir?
Cevap:
√144 = 12, çünkü 12² = 144’tür.
Şimdi her ifadeyi ayrı ayrı değerlendirelim:
I. √144 + 25 = 12 + 25 = 37 → rasyonel.
II. √144 − 25 = 12 − 25 = −13 → rasyonel.
III. √144 ÷ 25 = 12 ÷ 25 = 12/25 → rasyonel.
IV. √144 × 25 = 12 × 25 = 300 → rasyonel.
Dört ifadenin de sonucu tam sayı veya kesirli rasyonel sayı olduğu için hepsi rasyoneldir.
Sonuç: A) I, II, III ve IV
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 106 Cevapları MEB Yayınları
6.
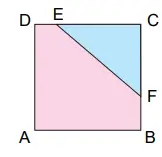
Yandaki ABCD karesel bölgenin alanı 243 santimetrekaredir.
|FB| / |FC| = 2/7 ve |DE| / |EC| = 1/8 olduğuna göre ECF üçgeninin alanı kaç santimetrekaredir?
Cevap:
Sağ kenar üzerindeki noktaya göre FC ve FB ilişkisi:
FB / FC = 2/7 ⇒ FB = (2/7)·FC.
Ayrıca FC + FB = s ⇒ FC + (2/7)FC = s ⇒ (9/7)FC = s ⇒ FC = (7/9)s.
(Böylece FB = s − FC = s − 7s/9 = 2s/9.)
Üst kenar üzerindeki noktaya göre DE ve EC ilişkisi:
DE / EC = 1/8 ⇒ DE = (1/8)·EC.
Ayrıca DE + EC = s ⇒ (1/8)EC + EC = s ⇒ (9/8)EC = s ⇒ EC = (8/9)s.
(Böylece DE = s − EC = s − 8s/9 = 1s/9.)
Üçgen ECF kenar uzunlukları (dik üçgen):
EC = 8s/9 (yatay), FC = 7s/9 (dikey).
Alan(ECF) = (1/2)·EC·FC = (1/2)·(8s/9)·(7s/9) = (1/2)·56·s²/81 = 28·s²/81.
s² = 243 olduğuna göre:
Alan = 28 · 243 / 81 = 28 · 3 = 84 cm².
Sonuç: B) 84 (Doğru)
7.
8√3, 10√2 ve 2√51 sayılarının büyükten küçüğe sıralanmış hâli seçeneklerden hangisinde doğru verilmiştir?
Cevap:
Her sayının karekökünü yaklaşık hesaplayalım:
√251 ≈ 15,8429795178
√102 ≈ 10,0995049384
√83 ≈ 9,1104335791
Dolayısıyla büyükten küçüğe sıralama: √251 > √102 > √83.
Sonuç: A) √251 > √102 > √83.
8.
√(3⁵) ifadesinin değeri aşağıdaki üslü ifadelerden hangisine daha yakındır?
Cevap:
Önce √(3⁵) ifadesini sadeleştirelim:
√(3⁵) = √(3⁴ × 3) = √(3⁴) × √3 = 3² × √3 = 9√3
√3 ≈ 1,732 olduğu için:
9√3 ≈ 9 × 1,732 = 15,588
Şimdi şıklardaki üslü ifadeleri hesaplayalım:
2² = 4 3² = 9 4² = 16 5² = 25
Bulduğumuz 15,588 sayısı 16’ya çok yakındır.
Sonuç: √(3⁵) ≈ 15,6 → en yakın üslü ifade 4² = 16’dır.
Sonuç: C) 4²
9.
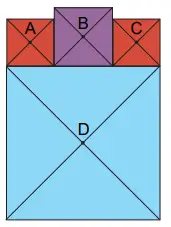
Yandaki şekilde kırmızı, mavi ve mor boyalı karesel bölgeler kenarları çakışacak şekilde birleştirilmiştir.
Kırmızı boyalı karesel bölgeler eşittir. A, B, C ve D noktaları bulundukları karesel bölgelerin köşegenlerinin kesişim noktalarıdır.
Kırmızı boyalı karesel bölgelerin her birinin alanı 24 santimetrekare, A ile C noktaları arasındaki en kısa mesafe ise 9√6 santimetredir.
Buna göre mavi boyalı karesel bölgenin alanı, mor boyalı karesel bölgenin alanından kaç santimetrekare fazladır?
Cevap:
Her kırmızı karenin alanı = 24 cm².
Kırmızı karenin kenarı r = √24 = 2√6.
Mor (ortadaki) karenin kenarına p diyelim.
Üstte soldaki kırmızı karenin merkezi A, sağdaki kırmızı karenin merkezi C; bu merkezler aynı yatay doğru üzerindedir.
A ile C arasındaki en kısa mesafe (yatay uzaklık) = 9√6 cm.
Mavi (alt) karenin kenarı S, mavi karenin genişliği üç üst karesinin toplam genişliğine eşittir: S = r + p + r = p + 2r.
A ile C arasındaki yatay uzaklığı ifade edelim.
Sol kırmızının merkezi x = r/2, sağ kırmızının merkezi x = r + p + r/2 = p + 3r/2.
Uzaklık = (p + 3r/2) − (r/2) = p + r.
Dolayısıyla p + r = 9√6.
r değerini yerine koyup p’yi bulalım.
r = 2√6 → p = 9√6 − 2√6 = 7√6.
Mavi karenin kenarı S = p + 2r = 7√6 + 2·(2√6) = 7√6 + 4√6 = 11√6.
Alanları hesaplayalım (karekökleri kare yaparak):
Mor karenin alanı = p² = (7√6)² = 49·6 = 294 cm².
Mavi karenin alanı = S² = (11√6)² = 121·6 = 726 cm².
İstenilen fark = mavi alanı − mor alanı = 726 − 294 = 432 cm².
Sonuç: 432 cm².
10.
√396 sayısının a√b biçiminde yazılmış hali aşağıdakilerden hangisi olabilir?
Cevap:
396’in asal çarpanlara ayrılmasını veya kare çarpan bulmayı deneyelim: 396 = 4 × 99 = 4 × 9 × 11 = 36 × 11.
√396 = √(36·11) = √36 · √11 = 6√11.
Sonuç: A) 6·√11.
8. Sınıf Matematik Ders Kitabı Sayfa 107 Cevapları MEB Yayınları
11.
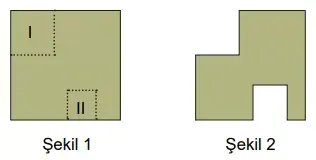
Şekil 1’de alanı 80 cm² olan karenin içerisinden alanı 45 cm² ve 20 cm² olan I ve II kare çıkarılmıştır.
Buna göre Şekil 2’nin çevre uzunluğu kaç santimetredir?
A) 12√5 B) 16√5 C) 20√5 D) 26√5
Cevap:
Büyük karenin alanı = 80 cm²
Kenar uzunluğu = √80 = 4√5 cm
I. karenin alanı = 45 cm² → kenar = 3√5 cm
II. karenin alanı = 20 cm² → kenar = 2√5 cm
Büyük karenin çevresi = 4 × 4√5 = 16√5 cm
I. karenin çevresi = 4 × 3√5 = 12√5 cm
II. karenin çevresi = 4 × 2√5 = 8√5 cm
Şekil 2’nin çevresi =
16√5 + 12√5 + 8√5 − 2 × (3√5 + 2√5)
= 36√5 − 10√5
= 26√5 cm
Sonuç: D) 26√5
12.
15√3 kilometre uzunluğundaki bir yolun 8 km’lik kısmında asfaltlama çalışması yapılmaktadır.
Buna göre yolun çalışma yapılmayan kısmının kilometre cinsinden uzunluğu hangi tam sayıya daha yakındır?
A) 16 B) 18 C) 20 D) 22
Cevap:
15√3 kilometre uzunluğundaki bir yolun 8 km’lik kısmı asfaltlanıyor.
Çalışma yapılmayan kısmın uzunluğunu bulalım:
1. İşlem:
Toplam uzunluk − asfaltlanan kısım = çalışma yapılmayan kısım
= 15√3 − 8
2. Yaklaşık değerle hesaplayalım:
√3 ≈ 1,732
15√3 ≈ 15 × 1,732 = 25,98
25,98 − 8 = 17,98
3. 17,98 ≈ 18
Sonuç: B) 18
13.
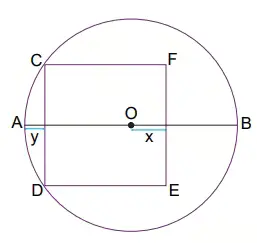
Yanda O merkezli çember ve DEFC karesi verilmiştir.
DEFC karesinin C ve D köşe noktaları O merkezli çemberin üzerindedir.
O merkezli çemberin iç bölgesinin alanı 6,75 santimetrekare, DEFC karesinin iç bölgesinin alanı 3,24 santimetrekaredir.
[AB] çapa ve [CF] // [AB] // [DE] ise x − y işleminin santimetre cinsinden değeri aşağıdakilerden hangisine eşittir?
(π = 3 alınız.)
A) 0,3 B) 0,4 C) 0,6 D) 0,9
Cevap:
Çemberin alanı = πR² = 6,75 ve π = 3 verilmiş.
πR² = 6,75 ⇒ 3·R² = 6,75 ⇒ R² = 6,75 / 3 = 2,25 ⇒ R = 1,5.
Karenin alanı = 3,24 ⇒ kenar uzunluğu s = √3,24 = 1,8. (Çünkü 1,8² = 3,24.)
Karenin sol üst köşesi C ve sol alt köşesi D çember üzerindedir. Karenin sol kenarının x-koordini = −d olsun. Sol köşe koordinatları (−d, ±s/2) çember denklemini sağlamalıdır:
d² + (s/2)² = R².
s/2 = 1,8/2 = 0,9.
d² + 0,9² = 1,5² ⇒ d² + 0,81 = 2,25 ⇒ d² = 1,44 ⇒ d = 1,2.
Yani karenin sol kenarı x = −1,2, karenin sağ kenarı x = −1,2 + 1,8 = 0,6.
Şimdi x ve y’yı resimdeki anlamlarına göre ifade edelim (resme bakılarak):
x: O merkezinden karenin sağ kenar orta noktasına olan yatay uzaklıktır. Bu uzaklık = 0,6 (adım 3’te bulduğumuz sağ kenar x-koordinatı).
y: Çemberin sol uç noktası ile karenin sol kenar orta noktası arasındaki uzaklıktır. Çemberin sol ucu AB üzerinde x = −R = −1,5; karenin sol kenarı orta noktası x = −d = −1,2. Aralarındaki uzaklık y = (−d) − (−R) = R − d = 1,5 − 1,2 = 0,3.
İstenen: x − y = 0,6 − 0,3 = 0,3.
Sonuç: A) 0,3.
14.
Aşağıdaki sayılardan hangisi √0,16 × √0,09 çarpımına eşittir?
Cevap:
√0,16 = 0,4 (çünkü 0,4² = 0,16).
√0,09 = 0,3 (çünkü 0,3² = 0,09).
Çarpım: 0,4 × 0,3 = 0,12.
0,12 bilimsel gösterimde = 12 × 10⁻².
Sonuç: C) 12 × 10⁻² (yani 0,12).
8. Sınıf Matematik Ders Kitabı Sayfa 108 Cevapları MEB Yayınları

Cevap:
1. Adım – Formül:
Bir yamuğun alanı,
Alan = ((a + b) / 2) × h
formülüyle bulunur.
Burada a ve b paralel kenarlardır, h ise yüksekliktir.
2. Adım – Değerleri yerine yazalım:
Alan = ((5√2 + 17√2) / 2) × 6√7
Önce parantez içini toplayalım:
5√2 + 17√2 = 22√2
Alan = (22√2 / 2) × 6√7
3. Adım – Sadeleştirme:
22√2 / 2 = 11√2
Alan = (11√2) × (6√7)
Katsayıları ve kökleri çarpalım:
11 × 6 = 66
√2 × √7 = √14
Alan = 66√14 cm²
Sonuç: Yamuğun alanı 66√14 cm²’dir.
16. Yanda beş doğru parçası ile yıldız oluşturulmuştur.
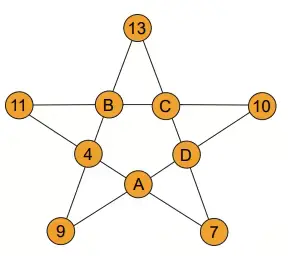
Doğru parçalarının kesişim noktalarına turuncu daireler konulmuştur. Yıldızı oluşturan her bir doğru parçasının üzerindeki turuncu dairelerin içindeki sayıların ayrı ayrı toplamı 28’dir.
Buna göre A,B,C ve D ifadelerine karşılık gelen değerler için aşağıdaki ifadelerden hangisi rasyonel sayıdır?
A) √A.B.C B) √A.C.D C) √A.B.D D) √B.C.D
Cevap:
Verilen: Yıldızı oluşturan her bir doğru parçasındaki turuncu dairelerdeki sayılar ayrı ayrı toplamı 28’dir. Dıştaki beş uç: 13 (üst), 11 (sol), 10 (sağ), 9 (alt-sol), 7 (alt-sağ). İç düğümlerde harflerle ve bir adet “4” var; harfler A (merkez), B (üst-sol iç), C (üst-sağ iç), D (alt-sağ iç). İçte sol altta verilen bir sayı 4’tür.
Beş doğru parçasının her birinin üzerinde dört sayı vardır; bu dört sayının toplamı 28’dir. Bunları tek tek yazalım (şekle bakarak hangi noktaların aynı doğru üzerinde olduğunu kullanalım):
1. Sol üstten başlayan eğik doğru: 13 + B + 4 + 9 = 28
→ 26 + B = 28 ⇒ B = 2.
2. Yatay üst doğru: 11 + B + C + 10 = 28
B = 2 olduğuna göre 11 + 2 + C + 10 = 28 ⇒ 23 + C = 28 ⇒ C = 5.
3. Sağ üstten inen eğik doğru: 13 + C + D + 7 = 28
C = 5 olduğuna göre 13 + 5 + D + 7 = 28 ⇒ 25 + D = 28 ⇒ D = 3.
4. Sol alt — sağ üst çapraz doğru: 11 + 4 + A + 7 = 28
⇒ 22 + A = 28 ⇒ A = 6.
5. Sağ alt — sol üst çapraz kontrolü: 10 + D + A + 9 = 10 + 3 + 6 + 9 = 28 (doğrulama sağlandı).
Bulduğumuz değerler: A = 6, B = 2, C = 5, D = 3.
Şimdi şıklardaki ifadelerin kareköklerinin rasyonel olup olmadığına bakalım (rasyonel olması için iç çarpımın tam bir tam kare olması gerekir):
A) √(A·B·C) = √(6·2·5) = √60 → irrasyonel.
B) √(A·C·D) = √(6·5·3) = √90 → irrasyonel.
C) √(A·B·D) = √(6·2·3) = √36 = 6 → rasyonel.
D) √(B·C·D) = √(2·5·3) = √30 → irrasyonel.
Sonuç: C) √(A·B·D) (çünkü √36 = 6 rasyoneldir).
17. Bir baraj gölünün altı ay boyunca su seviyesinin aylara göre değişimi yandaki grafikte verilmiştir.
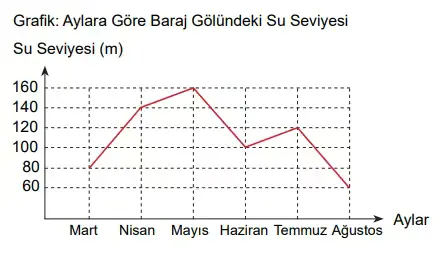
Verilen grafiğe göre bu altı ayın su seviyesinin ortalaması kaç metredir?
A) 105 B) 110 C) 120 D) 125
Cevap:
Verilenler (grafikten okunan değerler):
Mart: 80 m
Nisan: 140 m
Mayıs: 160 m
Haziran: 100 m
Temmuz: 120 m
Ağustos: 60 m
Çözüm:
Altı ayın su seviyesinin ortalamasını bulmak için, tüm ayların su seviyelerini toplayıp 6’ya böleceğiz:
Ortalama = (80 + 140 + 160 + 100 + 120 + 60) / 6
Önce toplamı hesaplayalım:
80 + 140 = 220
220 + 160 = 380
380 + 100 = 480
480 + 120 = 600
600 + 60 = 660
Şimdi ortalamayı bulalım:
Ortalama = 660 / 6 = 110 m
Bu değer, B seçeneğine tam olarak karşılık gelir.
Sonuç: B) 110
8. Sınıf Matematik Ders Kitabı Sayfa 109 Cevapları MEB Yayınları
18 Bir yolcu otobüsünde bulunan yolcuların %45’i erkek, %35’i kadın ve geriye kalanı çocuktur.
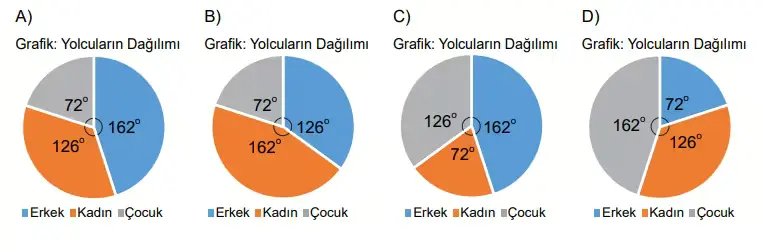
Bu verilere ait daire grafiği aşağıdakilerden hangisidir?
Cevap:
Verilenler:
Erkek %45
Kadın %35
Çocuk %20 (çünkü %100 − 45 − 35 = 20)
1. Adım – Daire grafiğinde açı hesaplama
Bir daire 360° olduğuna göre,
Erkek: 360 × 45 / 100 = 162°
Kadın: 360 × 35 / 100 = 126°
Çocuk: 360 × 20 / 100 = 72°
2. Adım – Grafiğe göre renk eşleşmesi
Grafiklerde:
Mavi → Erkek
Turuncu → Kadın
Gri → Çocuk
Bu durumda doğru grafikte:
Mavi dilim 162° olmalı
Turuncu dilim 126° olmalı
Gri dilim 72° olmalı
3. Adım – Şıklara bakış
Bu düzen A şıkkında doğru verilmiştir.
Sonuç: A)
19. (√0.36 + √0.04) / (√1.21 + √0.25) işleminin sonucu aşağıdakilerden hangisine eşittir?
Cevap:
√1,21 = 1,1 (çünkü 1,1² = 1,21).
√0,25 = 0,5 (çünkü 0,5² = 0,25).
√0,36 = 0,6 (çünkü 0,6² = 0,36).
√0,04 = 0,2 (çünkü 0,2² = 0,04).
Toplam: 1,1 + 0,5 + 0,6 + 0,2 = 2,4.
Sonuç: 2,4.
20. Aynı gün dikilen bir meyve ağacının farklı üç türünün dikildiği günden itibaren geçen yıllara göre ulaştığı verim aşağıdaki sütun grafiğinde verilmiştir.
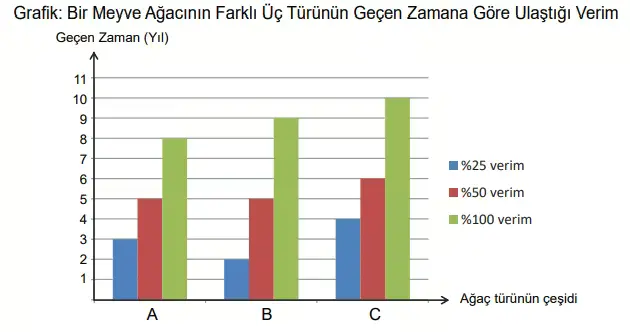
Buna göre %25 verime ulaştıktan en az kaç yıl sonra dikilen ağaç türlerinden herhangi biri %100 verime ulaşmış olur?
A) 3 B) 4 C) 5 D) 6
Cevap:
Verilenler:
A türü ağaç:
%25 verime ulaştığı yıl: 3. yıl
%100 verime ulaştığı yıl: 8. yıl
B türü ağaç:
%25 verime ulaştığı yıl: 2. yıl
%100 verime ulaştığı yıl: 9. yıl
C türü ağaç:
%25 verime ulaştığı yıl: 4. yıl
%100 verime ulaştığı yıl: 10. yıl
Çözüm:
Her bir ağaç türü için %25 verimden %100 verime ulaşana kadar geçen süreyi hesaplayalım:
A türü için: 8 – 3 = 5 yıl
B türü için: 9 – 2 = 7 yıl
C türü için: 10 – 4 = 6 yıl
Bu hesaplamalara göre, %25 verime ulaştıktan sonra en kısa sürede %100 verime ulaşan ağaç A türüdür ve bu süre 5 yıldır.
Sonuç: C) 5