8. Sınıf Matematik Ders Kitabı Sayfa 108-109-110-111. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 108-109-110-111. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 108-109-110-111 konularına ait cevapları bulabilirsiniz. “2. Ünite Değerlendirme Soruları Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 108-109-110-111. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
2. Ünite Değerlendirme Soruları Cevapları
2. Ünite Kareköklü İfadeler Veri Analizi: Karekök işlemlerinde tam kare sayıların karekökleri tam sayı olarak bulunur, diğer sayıların karekökleri ise iki tam sayı arasında yer alır. Grafikler ise verilerin görsel olarak daha kolay anlaşılmasını ve karşılaştırılmasını sağlar.
Sonraki Sayfalar: 112-113-114-115-116
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 108. Cevapları Sonuç Yayınları
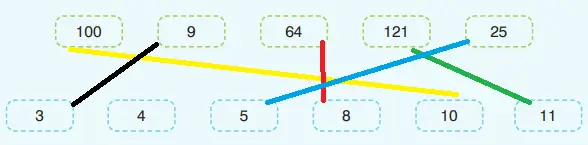
1) Kutucuklarda verilen sayılardan tam kare pozitif tam sayı olanlar ile bunların karekök değerleri eşleştirildiğinde hangi sayı açıkta kalır? Yazınız.
Cevap:
Verilen tam kare sayılar: 100, 9, 64, 121, 25
Verilen karekök adayları: 3, 4, 5, 8, 10, 11
Karekök işlemleri:
√100 = 10
√9 = 3
√64 = 8
√121 = 11
√25 = 5
Eşleşenler: 3, 5, 8, 10, 11
Açıkta kalan: 4
2) İfadelerdeki noktalı yerlere uygun doğal sayıları yazınız.
Cevap:
a) √96
9² = 81, 10² = 100
96 bu ikisinin arasındadır.
Yaklaşık √96 ≈ 9,79796
En yakın doğal sayı: 10
b) √80
8² = 64, 9² = 81
80 bu ikisinin arasındadır ve 81’e daha yakındır.
Yaklaşık √80 ≈ 8,94427
En yakın doğal sayı: 9
c) √200
14² = 196, 15² = 225
200 bu ikisinin arasındadır.
Yaklaşık √200 ≈ 14,1421
En yakın doğal sayı: 14
ç) √30
5² = 25, 6² = 36
30 bu ikisinin arasındadır.
Yaklaşık √30 ≈ 5,4772
En yakın doğal sayı: 5
d) √300
17² = 289, 18² = 324
300 bu aralıktadır.
144 < 300 < 324
Bu yüzden √300 17 ile 18 arasındadır.
e) √146
12² = 144, 13² = 169
146 bu aralıktadır.
144 < 146 < 169
Bu yüzden √146 12 ile 13 arasındadır.
f) √101
10² = 100, 11² = 121
101 bu aralıktadır.
100 < 101 < 121
Bu yüzden √101 10 ile 11 arasındadır.
g) √170
13² = 169, 14² = 196
170 bu aralıktadır.
169 < 170 < 196
Bu yüzden √170 13 ile 14 arasındadır.

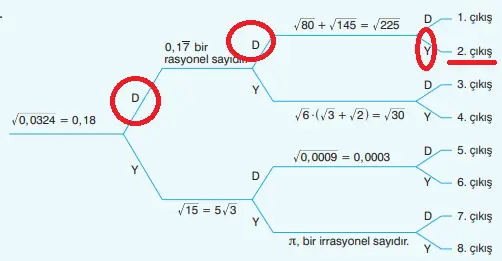
3) Yukarıda verilen şemadaki ifadeleri en soldan başlayarak inceleyiniz. İfadeler doğru ise “D”, yanlış ise “Y” yolunu takip ediniz. Kaçıncı çıkışa ulaştınız? Yazınız.
Cevap:
1. İfade: √0,0324 = 0,18
0,18² = 0,0324 → Doğru → “D” yolundan git
2. İfade: 0,17 bir rasyonel sayıdır.
0,17 = 17/100 → rasyoneldir → Doğru → “D” yolundan git
3. İfade: √80 + √145 = √225
√225 = 15
√80 ≈ 8,9443
√145 ≈ 12,0416
Toplam ≈ 20,9859
20,9859 ≠ 15 → Yanlış → “Y” yolundan git
“Y” yolu 2. çıkışa yönlendirir.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 109. Cevapları Sonuç Yayınları
4) Yandaki düzgün sekizgenin çevre uzunluğu √320 cm’dir. Buna göre düzgün sekizgenin bir kenar uzunluğu kaç cm’dir?
Cevap:
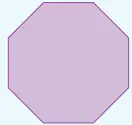
Düzgün sekizgenin çevresi: √320 cm
Bir kenar = çevre / 8
√320’yi sadeleştirelim:
320 = 64 × 5
√320 = √(64×5) = 8√5
Kenar uzunluğu = (8√5) / 8 = √5
5) Aşağıdaki eşitliklerde verilen □ sembolünün içine yazılması gereken doğal sayıları bulunuz.
Cevap:
a) 7√3 = √□
Her iki tarafın karesini al:
(7√3)² = 49 × 3 = 147
□ = 147
b) 6√□ = √108
Her iki tarafın karesini al:
36 × □ = 108
□ = 108 / 36 = 3
c) 3√□ = √45
Karesini al:
9 × □ = 45
□ = 5
ç) 10√5 = √□
Karesini al:
100 × 5 = 500
□ = 500
d) □√5 = √20
Karesini al:
(□²)(5) = 20
□² = 20 ÷ 5 = 4
□ = 2
e) □√2 = √98
Karesini al:
(□²)(2) = 98
□² = 98 ÷ 2 = 49
□ = 7
f) √□ = 10√2
Karesini al:
□ = 100 × 2 = 200
g) 4√□ = √32
Karesini al:
16 × □ = 32
□ = 2
Cevap listesi:
- a) 147
- b) 3
- c) 5
- ç) 500
- d) 2
- e) 7
- f) 200
- g) 2
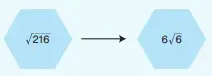
6) Yandaki ABCD paralelkenarında |DH | = 2√3 cm, | AB | = 3√2 cm ve [AB] 1 [DH] ise ABCD paralelkenarının alanı kaç cm2 dir?
Cevap: B)
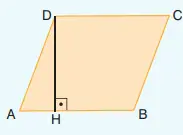
Verilenler:
|DH| = 2√3
|AB| = 3√2
AB ⟂ DH → bunlar dik
Paralelkenar alanı = taban × yükseklik
= (3√2) × (2√3)
İşlem:
3 × 2 × √2 × √3
= 6 × √6
Sonuç: B) 6√6
7) √176 ifadesi aşağıdakilerden hangisi ile çarpılırsa işlem sonucu bir doğal sayı olur?
Cevap: D)
√176 sadeleştirelim:
176 = 16 × 11
√176 = 4√11
Doğal sayı olması için içerdeki √11’in yok olması gerekir → √11 ile çarpılır.
4√11 × √11 = 4 × 11 = 44 (doğal sayı)
Sonuç: D) √11
8) Öğrencilerin belirttiği ifadelerin toplamı aşağıdakilerden hangisidir?
Cevap: A)

Verilen ifadeler:
√180
−√45
−2√5
√363
Her birini sadeleştirelim:
√180 = √(36×5) = 6√5
√45 = √(9×5) = 3√5 → −√45 = −3√5
−2√5 → aynen kalır
√363 = √(121×3) = 11√3
Şimdi hepsini toplayalım:
6√5
−3√5
−2√5
11√3
√5’li olanlar:
6√5 − 3√5 − 2√5 = 1√5
Geriye:
√5 + 11√3
Sonuç: A) √5 + 11√3
8. Sınıf Matematik Ders Kitabı Sayfa 110. Cevapları Sonuç Yayınları
9) Yandaki şemada belirtilen işlemleri yaparak renkli kutucuklara cevapları yazınız.
Cevap:
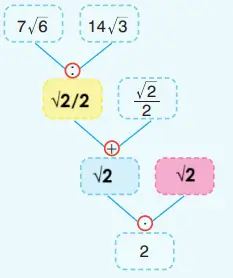
Üst işlem (bölme):
7√6 ÷ 14√3
= (7/14) · (√6/√3)
= 1/2 · √(6/3)
= 1/2 · √2
Sarı kutu = √2/2
Orta işlem (toplama):
Sarı kutu + sağdaki √2/2
= √2/2 + √2/2
= √2
Mavi kutu = √2
Alt işlem (çarpma):
Mavi kutu · (pembe kutu) = 2
√2 · (pembe) = 2
pembe = 2 / √2 = √2
Pembe kutu = √2
Sonuçlar:
Sarı kutu = √2/2
Mavi kutu = √2
Pembe kutu = √2
10) 3√▲ : √2 = 6 olduğuna göre ▲ yerine hangi doğal sayı yazılmalıdır?
Cevap: B)
3√▲ / √2 = 6
3√▲ = 6√2
√▲ = 2√2
Karesini al: ▲ = (2√2)² = 4 · 2 = 8
Sonuç: B) 8
11) Serbest paraşütçü olan Cemre Hanım, yerden /2048 m yükseklikteki atlama kulesinden paraşütle atlar. Cemre Hanım, 20/2 m aşağı indikten sonra paraşütünü açar. Buna göre Cemre Hanım, paraşütünü açtığında yerden kaç metre yükseklikte olur?
Cevap:

√2048 = √(1024·2) = 32√2
İniş = 20√2
Kalan yükseklik = 32√2 − 20√2 = 12√2
Sonuç: 12√2 m
12) Erdinç, Salim ve İpek’in belirli vakitlerde ölçülen vücut sıcaklıkları, yandaki üçlü çizgi grafiğinde verilmiştir. Çizgi grafiğine göre aşağıdaki soruları cevaplayınız.
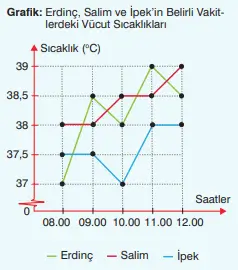
a) Saat 08.00’de kimin vücut sıcaklığı diğerlerinden daha fazladır?
Cevap: 08:00: Salim 38,0 en yüksek. Sonuç: Salim
b) Hangi saatlerde Salim’in vücut sıcaklığı, Erdinç ile İpek’in vücut sıcaklığından daha fazladır?
Cevap: Karşılaştırma:
08:00 → Salim (38,0) > Erdinç (37,0) ve > İpek (37,5) → evet
09:00 → Salim (38,0) < Erdinç (38,5) → hayır 10:00 → Salim (38,5) > Erdinç (38,0) ve > İpek (37,0) → evet
11:00 → Salim (38,5) < Erdinç (39,0) → hayır 12:00 → Salim (39,0) > Erdinç (38,5) ve > İpek (38,0) → evet
Sonuç: 08:00, 10:00 ve 12:00
c) Erdinç’in vücut sıcaklığındaki en büyük artış, hangi saatler arasında olmuştur?
Cevap:
Erdinç: 08:00→09:00 artış 1,5° (37,0→38,5)
09:00→10:00 azalma, 10:00→11:00 artış 1,0° (38,0→39,0)
En büyük artış 08:00–09:00 (1,5 °C).
Sonuç: 08:00–09:00
ç) Saat 12.00’de Salim ile İpek’in vücut sıcaklıkları arasındaki fark kaç °C’tur?
Cevap:
12:00: Salim 39,0 ; İpek 38,0 → fark = 1,0 °C
Sonuç: 1,0 °C
d) Erdinç’in vücut sıcaklığının en düşük değeri saat kaçta olmuştur?
Cevap:
Erdinç’in en düşük değeri 37,0 °C → saat 08:00.
Sonuç: 08:00
8. Sınıf Matematik Ders Kitabı Sayfa 111. Cevapları Sonuç Yayınları
13) A, B ve C şirketlerinin ürettiği kazakların renklere göre sayıları, yandaki üçlü sütun grafiğinde gösterilmiştir. Sütun grafiğine göre aşağıdaki soruları cevaplayınız.
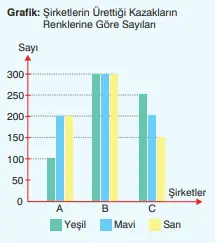
a) Eşit sayıda yeşil, mavi ve sarı kazak üreten şirket toplam kaç kazak üretmiştir?
Cevap: Sadece B şirketi, üç rengin hepsinden 300 tane üretmiştir.
Toplam = 300 (yeşil) + 300 (mavi) + 300 (sarı)
Toplam = 900 Kazak
b) C şirketi toplam kaç sarı ve mavi kazak üretmiştir?
Cevap:
C sarı = 150 kazak, C mavi = 200 kazak
Toplam = 150 kazak + 200 kazak
Toplam = 350 kazak
ç) B ile A şirketlerinin ürettiği kazak sayılarının arasındaki fark kaçtır?
Cevap:
A yeşil = 100 kazak, B yeşil = 300 kazak, C yeşil = 250 kazak
Toplam yeşil = 100 kazak + 300 kazak + 250 kazak
Toplam yeşil = 650 kazak
ç) B ile A şirketlerinin ürettiği kazak sayılarının arasındaki fark kaçtır?
Cevap:
A toplam = A yeşil + A mavi + A sarı
A toplam = 100 kazak + 200 kazak + 200 kazak = 500 kazak
B toplam = B yeşil + B mavi + B sarı
B toplam = 300 kazak + 300 kazak + 300 kazak = 900 kazak
Fark = B toplam − A toplam
Fark = 900 kazak − 500 kazak = 400 kazak
14) Fotoğrafçılık kulübü öğrencisi Eda’nın çektiği fotoğrafların aylara göre sayıları, yandaki sütun grafiğinde gösterilmiştir. Sütun grafiğindeki verileri çizgi grafiğinde gösteriniz.
Cevap:
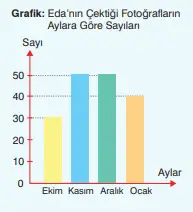
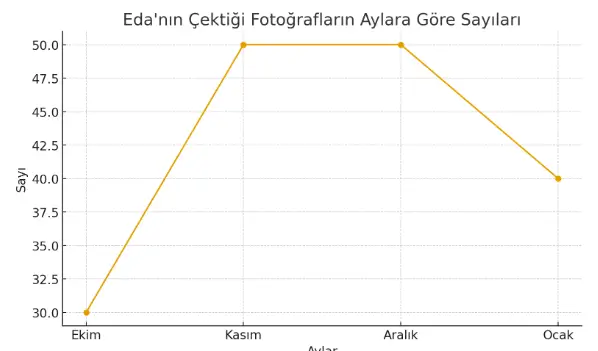
Eda’nın aylara göre çektiği fotoğraf sayıları sütun grafiğinden alınarak çizgi grafiğinde gösterilmiştir.
Buna göre:
- Ekim ayında 30 fotoğraf,
- Kasım ayında 50 fotoğraf,
- Aralık ayında 50 fotoğraf,
- Ocak ayında 40 fotoğraf çektiği çizgi grafiğinde işaretlenmiştir.
15) Bir kırtasiyede satılan tükenmez kalem sayılarının renklerine göre dağılımı, yandaki daire grafiğinde gösterilmiştir. Kırtasiyede toplam 600 tükenmez kalem satılmıştır. Buna göre daire grafiğindeki verileri sütun grafiğinde gösteriniz.
Cevap:
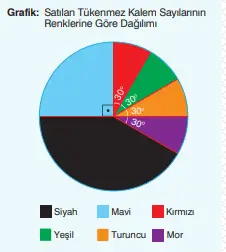
Toplam satılan tükenmez kalem = 600 kalem
Daire grafiği açıları:
- Siyah dilim = 150°
- Mavi dilim = 90°
- Kırmızı dilim = 30°
- Yeşil dilim = 30°
- Turuncu dilim = 30°
- Mor dilim = 30°
Genel formül:
Renk sayısı (kalem) = 600 × (Renk açısı / 360)
Hesaplar:
- Siyah:
600 × 150/360 = 600 × (5/12) = 600 ÷ 12 × 5 = 50 × 5 = 250 kalem - Mavi:
600 × 90/360 = 600 × (1/4) = 600 ÷ 4 = 150 kalem - Kırmızı:
600 × 30/360 = 600 × (1/12) = 600 ÷ 12 = 50 kalem - Yeşil: aynı 30° → 50 kalem
- Turuncu: aynı 30° → 50 kalem
- Mor: aynı 30° → 50 kalem
Kontrol: 250 + 150 + 50 + 50 + 50 + 50 = 600 kalem ✓
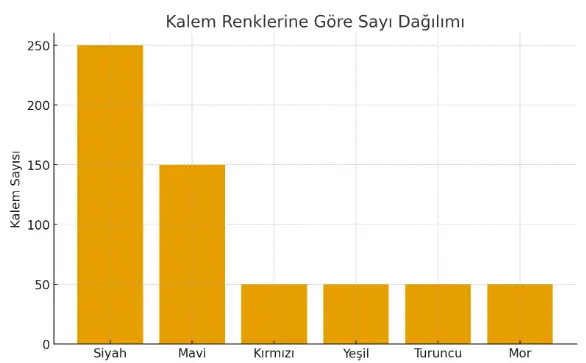
Sütun grafiği için sayılar:
- Siyah: 250 kalem
- Mavi: 150 kalem
- Kırmızı: 50 kalem
- Yeşil: 50 kalem
- Turuncu: 50 kalem
- Mor: 50 kalem
Sonraki Sayfalar: 112-113-114-115-116