8. Sınıf Matematik Ders Kitabı Sayfa 112-113-114-115-116. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 112-113-114-115-116. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 112-113-114-115-116 konularına ait cevapları bulabilirsiniz. “2. Ünite Değerlendirme Soruları Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 112-113-114-115-116. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
2. Ünite Değerlendirme Soruları Cevapları
2. Ünite Kareköklü İfadeler Veri Analizi: Kareköklü ifadelerle yapılan hesaplamalarda, çokgenlerin kenar sayıları ve alan ilişkisi matematiksel çözümlerde önemli bir rol oynar. Bu tür problemlerde köklerin sadeleştirilmesi ve geometrik özelliklerin kullanılması gerekir.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 112. Cevapları Sonuç Yayınları
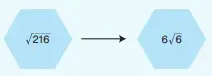
16) Yukarıda verilen çokgenin içinde bulunan kareköklü ifadeler a√b şeklinde yazılıyor, b değeri, kareköklü ifadenin içinde bulunduğu çokgenin kenar sayısına eşit oluyor.
Aynı özellikleri taşıyan yukarıdaki çokgende bulunan D yerine aşağıdaki ifadelerden hangisi yazılabilir?
Cevap: Çokgendeki kareköklü ifade a√b olarak yazılıyor ve b = çokgenin kenar sayısı.
Örnekte:
√216 → 6√6
Burada b = 6, şekil altıgen.
D harfi 7 kenarlı çokgende olduğuna göre b = 7 olmalı.
Seçenekleri kontrol:
- √98 = 7√2 → b = 2 (uymaz)
- √115 → içinde 7 yok (uymaz)
- √175 = √(25×7) = 5√7 → b = 7 (uyar)
- √225 = 15 (kök değil, uymaz)
Sonuç: C) √175
17) Uzun kenarı 36√2 dm uzunluğunda olan dikdörtgen şeklindeki panoya aşağıdaki görselde olduğu gibi dikdörtgen şeklindeki 3 eş afiş, kenarları panonun kenarlarına paralel olacak şekilde asılmıştır.
Görselde verilen her bir afişin uzun kenar uzunluğu, kısa kenar uzunluğunun 2 katıdır. Görselde verilenlere göre her bir afişin bir yüzünün alanı kaç dm2dir?
Cevap:
Pano uzun kenarı = 36√2
4 tane boşluk var:
Her biri √18 = 3√2 → toplam boşluk: 12√2
Afişlerin toplamı:
36√2 − 12√2 = 24√2
3 afiş olduğuna göre:
Bir afiş uzun kenarı = 24√2 ÷ 3 = 8√2
Uzun kenar, kısa kenarın 2 katı:
Kısa kenar = (8√2) ÷ 2 = 4√2
Alan = (8√2)(4√2)
= 32 × 2
= 64 dm²
Sonuç: B) 64
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 113. Cevapları Sonuç Yayınları
18) Semih, en fazla 300 kg yük taşıyabilen bir asansöre her birinin kütlesi 5√10 kg olan kutularla birlikte binecektir. Semih’in asansörle taşıması gereken 14 kutu vardır.
Semih’in kütlesi 90 kg olduğuna göre Semih, tek seferde asansöre bu kutulardan en fazla kaç tanesi ile binebilir?
Cevap:
1) Asansöre kutular için kalan ağırlık:
300 − 90 = 210 kg
2) Bir kutunun yaklaşık kütlesi:
√10 yaklaşık 3,16’dır.
5 × 3,16 = 15,8 kg
3) Alınabilecek kutu sayısı:
210 ÷ 15,8 = 13,2
Tam sayı olarak 13 kutu taşınabilir.
19) A noktasında bulunan Sinan’ın D noktasına giderken izlediği güzargah aşağıda verilmiştir.
A ile B noktaları arasındaki uzaklık 10 km’dir. A ile B noktaları arasındaki uzaklık, B ile C noktaları arasındaki uzaklığın√2 katı; C ile D noktaları arasındaki uzaklık, B ile C noktaları arasındaki uzaklığın 2 katıdır.
Sinan, D noktasına ulaştıktan sonra aynı güzergâhı takip ederek A noktasına geri dönmüştür.
Buna göre Sinan, A noktasına geri döndüğünde toplam kaç kilometre yol gitmiş olur?
Cevap:
1) B–C uzunluğunu bulalım.
A–B = 10
A–B = √2 × B–C
10 = √2 × B–C
B–C = 10 ÷ √2 = 5√2
2) Diğer uzaklıklar:
A–C = A–B + B–C
A–C = 10 + 5√2
C–D = 2 × B–C
C–D = 10√2
3) Gidiş yolu:
A–B + B–C + C–D
= 10 + 5√2 + 10√2
= 10 + 15√2
4) Gidiş–dönüş toplamı:
(10 + 15√2) × 2
= 20 + 30√2
Sonuç: C) 20 + 30√2
8. Sınıf Matematik Ders Kitabı Sayfa 114. Cevapları Sonuç Yayınları
20) Bir kenar uzunluğu a birim olan bir karenin köşegen uzunluğu a√2 birimdir.
Kayra, kare şeklindeki üç kartonu aşağıdaki gibi yan yana koyuyor.
3. kartonun kenar uzunluğu, 2. kartonun kenar uzunluğunun √3 katı;
2. kartonun kenar uzunluğu, 1. kartonun kenar uzunluğunun √3 katıdır.
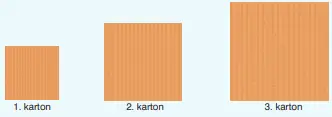
1. kartonun köşegen uzunluğu 18 cm olduğuna göre 3. kartonun köşegen uzunluğu kaç santimetredir?
Cevap:
1. kartonun köşegen uzunluğu = 18 cm
Bir karenin köşegeni:
kenar × √2
Bu yüzden:
18 = a₁ × √2
a₁ = 18 ÷ √2 = 9√2 cm
2. kartonun kenarını bulalım
2. karton = 1. karton × √3
a₂ = 9√2 × √3
√2 × √3 = √6
a₂ = 9√6 cm
3. kartonun kenarını bulalım
3. karton = 2. karton × √3
a₃ = 9√6 × √3
√6 × √3 = √18
√18 = 3√2
a₃ = 9 × 3√2 = 27√2 cm
3. kartonun köşegenini bulalım
Köşegen = kenar × √2
= 27√2 × √2
√2 × √2 = 2
27 × 2 = 54 cm
Sonuç: D) 54
21) Alanı 105 m2 olan kare şeklindeki aşağıda verilen oyun parkının çevresine 3 sıra tel çekilecektir.
Telin metre fiyatının satın alınacak miktara göre değişimi aşağıda gösterilmiştir.
Buna göre bu iş için kullanılacak telin metresi kaç TL olur?
Cevap:
Park kare olduğuna göre:
Alan = kenar × kenar = 105 m²
Kenar uzunluğu:
kenar = √105
Parkın çevresi
Çevre = 4 × kenar
= 4√105
3 sıra tel çekilecek
Toplam tel:
3 × 4√105 = 12√105 metre
√105 ≈ 10,24 olduğu için:
12 × 10,24 ≈ 122,9 m
→ Yaklaşık 123 m tel gerekir.
Fiyat tablosuna göre
123 m, 110 – 149 m aralığına girer.
Bu aralıkta metre fiyatı: 120 TL
Sonuç: B) 120
8. Sınıf Matematik Ders Kitabı Sayfa 115. Cevapları Sonuç Yayınları
22) Aziz dede, arsasını dört çocuğuna aşağıdaki grafikte gösterilen oranlarda paylaştırmıştır.
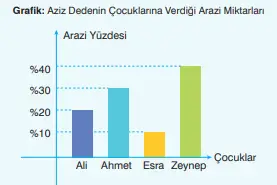
Bu çocuklardan Zeynep, kendine verilen arsayı üç çocuğuna aşağıda verilen oranlarda dağıtmıştır.
Grafik: Zeynep’in, Çocuklarına Verdiği Arazi Miktarlarının Dağılımı
Burak, kendi payına düşen arsanın % 60’ına ev yapmış geri kalan kısmını ise yeşil alan olarak ayırmıştır.
Burak’ın yeşil alan olarak ayırdığı alan 120 m² olduğuna göre Aziz dede oğlu Ahmet’e kaç m² arsa vermiştir?
Cevap:
Verilenler (özet):
- Aziz dede toplam arazi = T m².
- Zeynep’e verilen pay = %40 of T = 0,40·T.
- Zeynep’in çocuklarına verdiği açılar: Baran 140°, Beyza 100°, Burak 120°.
Bu açıların oranı = açı/360 ile hesaplanır. Burak’ın oranı = 120/360 = 1/3. - Burak, kendi payının %60’ını eve ayırmış; kalan %40’ı yeşil alan.
- Burak’ın yeşil alanı = 120 m² verilmiş.
1) Burak’ın başlangıçta aldığı arsa (Zeynep’in payı içinden):
Zeynep’in payı = 0,40·T.
Burak bu payın 1/3’ünü alır → Burak’ın payı = (1/3)·0,40·T = 0,40·T / 3 = 2/15·T.
(Çünkü 0,40 = 2/5 ve (1/3)·(2/5) = 2/15.)
2) Burak’ın yeşil alanı (kalanı):
Burak’ın yeşil alanı = Burak’ın payının %40’ı = 0,40 · (2/15·T) = (2/15)·0,40·T = 4/75·T.
Bu miktar = 120 m² olarak verilmiş.
Yani 4/75·T = 120 m².
3) Toplam araziyi bulalım:
T = 120 · (75/4)
120 ÷ 4 = 30 → 30 × 75 = 2250
Toplam arazi T = 2250 m².
4) Ahmet’e verilen arsa:
Grafiğe göre Ahmet’in payı = %30 → Ahmet’in alanı = 0,30 · T = 0,30 · 2250 = 675 m².
Sonuç: D) 675 m²
8. Sınıf Matematik Ders Kitabı Sayfa 116. Cevapları Sonuç Yayınları
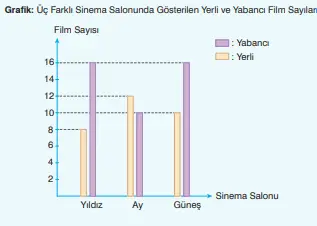
23) Yıldız, Ay ve Güneş sinema salonlarında mart ayı içinde gösterilen yerli ve yabancı film sayıları aşağıdaki sütun grafiğinde verilmiştir.
Buna göre
I. Üç salonda oynatılan toplam yerli film sayısı 30’dur.
II. Üç salonda oynatılan toplam yabancı film sayısı 42’dir.
III. En az film oynatılan salondaki film sayısı 22’dir.
ifadelerinden hangileri doğrudur?
Cevap:
I. Üç salondaki toplam yerli film sayısı 30’dur.
Toplam yerli =
8 (Yıldız) + 12 (Ay) + 10 (Güneş) = 30
→ Doğru
II. Üç salondaki toplam yabancı film sayısı 42’dir.
Toplam yabancı =
16 (Yıldız) + 10 (Ay) + 16 (Güneş) = 42
→ Doğru
III. En az film oynatan salondaki film sayısı 22’dir.
Salon toplamları =
24, 22, 26 → en küçük sayı 22
→ Doğru
Sonuç: Üçü de doğru → D) I, II ve III
24) Kenar uzunlukları verilen aşağıdaki dikdörtgenlerden hangisinin alanı m2 cinsinden tam sayı belirtmez.
Cevap:
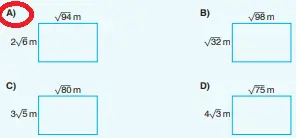
A şıkkı: kısa kenar = 2√6, uzun kenar = √94
Alan = (2√6) × (√94) = 2 × √(6×94) = 2 × √564.
Şimdi 564’ü kontrol edelim:
564 = 4 × 141 = 4 × 3 × 47. Burada 141 = 3 × 47 ve 47 asal. Yani 564’ün çarpanlarının içinde tam ikili kare çarpanlar (ör. 9, 25, 49 vb.) yok (sadece 4 eşli). √564 ≠ tam sayı, dolayısıyla 2×√564 de tam sayı değil.
→ A şıkkı alanı tam sayı vermez.
B şıkkı: kısa kenar = √32, uzun kenar = √98
Alan = √32 × √98 = √(32×98) = √3136.
3136 = 56 × 56 (çünkü 50²=2500, 56²=3136). Yani √3136 = 56 → alan = 56 (tam sayı).
→ B şıkkı tam sayı verir.
C şıkkı: kısa kenar = 3√5, uzun kenar = √80
Alan = 3√5 × √80 = 3 × √(5×80) = 3 × √400.
√400 = 20, dolayısıyla alan = 3 × 20 = 60 (tam sayı).
→ C şıkkı tam sayı verir.
D şıkkı: kısa kenar = 4√3, uzun kenar = √75
Alan = 4√3 × √75 = 4 × √(3×75) = 4 × √225.
√225 = 15, dolayısıyla alan = 4 × 15 = 60 (tam sayı).
→ D şıkkı tam sayı verir.
Sonuç: A şıkkındaki çarpım kare sayı yapmadığı için A seçeneği alanı tam sayı vermez.
(B, C, D seçenekleri tam sayı alan verir.)
Sonraki Ödevler
