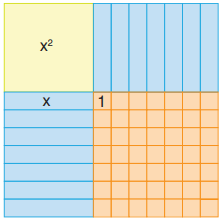8. Sınıf Matematik Ders Kitabı Sayfa 129-132-138-139. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 129-132-138-139. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 129-130-131-132-133-134-135-136-137-138-139 konularına ait cevapları bulabilirsiniz. “Basit Cebirsel İfadeler ve Cebirsel İfadelerle Çarpma İşlemi Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 129-132-138-139. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Basit Cebirsel İfadeler ve Cebirsel İfadelerle Çarpma İşlemi Cevapları
3. Ünite Cebirsel İfadeler ve Özdeşlikler: Cebirsel ifadeler, matematikte değişkenler ve sayılar arasındaki ilişkileri göstermek için kullanılır. Çarpma ve toplama işlemleriyle bu ifadeleri düzenleyerek geometrik şekillerin alanlarını veya denklem çözümlerini bulabiliriz.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 129. Cevapları Sonuç Yayınları

780 ile 850 yılları arasında yaşayan Müslüman ilim insanı Muhammed İbni Musa Al-Hârezmî; matematik, astronomi ve coğrafya alanlarında çalışmalar yapmış ve bu alanlarda eserler ortaya koymuştur.
Hârezmî, en ünlü eseri olan “El Kitab’ul Muhtasar fi’l Hesab’il Cebri ve’l Mukabele”de, cebir konularını ele almıştır ve bu eser, ileriki zamanlarda dünyada cebir bilimine temel olmuştur.
Cebir alanında çalışma yapan diğer bilim insanlarını araştırınız.
Cevap:
• Ömer Hayyam (1048–1131)
Üçüncü dereceden denklemler üzerinde çalışmış, cebirin gelişmesine büyük katkı sağlamıştır.
• Ebu Kâmil Şucâ el-Mısrî (850–930)
Cebiri sistemli hâle getiren matematikçilerdendir. Hârezmî’nin çalışmalarını geliştirmiştir.
• Sabit bin Kurra (836–901)
Cebir ve sayı teorisi üzerine önemli çalışmalar yapmıştır.
• İbn Sina (980–1037)
Felsefe ve tıpla birlikte matematikte, özellikle cebirde önemli yorumlar yazmıştır.
• Nasîrüddin Tûsî (1201–1274)
Cebir ve trigonometri alanında önemli eserler vermiştir.
• İbnü’l-Bennâ el-Merrakeşî (1256–1321)
Aritmetik ve cebir alanında eserler yazmış, denklem çözümlerini geliştirmiştir.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 132. Cevapları Sonuç Yayınları
Etkinlik
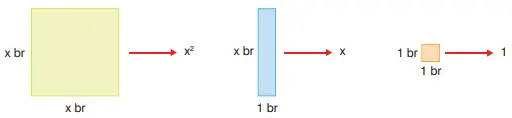
Araç Gereç: Cebir karoları
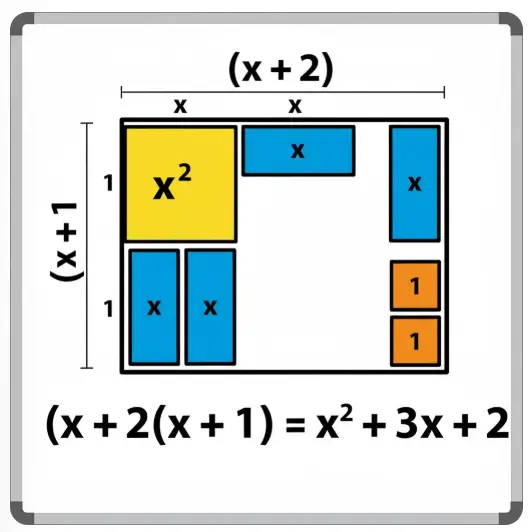
Bazı cebirsel ifadelerle temsil edilen yukarıdaki cebir karolarını kullanarak bir dikdörtgeni modelleyiniz.
Cevap:
Dikdörtgen, 1 tane x^2 karosu, 3 tane x karosu ve 2 tane 1’lik karonun bir araya getirilmesiyle oluşturulur.
Dikdörtgen modelindeki uzun ve kısa kenar uzunluklarını belirten cebirsel ifadeleri yazınız.
Cevap:
Uzun kenar: x + 2
Kısa kenar: x + 1
Dikdörtgen modelindeki uzun ve kısa kenar uzunluklarını çarpma işlemi şeklinde yazınız.
Cevap:
Dikdörtgenin alanı çarpma şeklinde:
(x + 2)(x + 1)
Dikdörtgen modelini oluşturan cebir karolarının belirttiği cebirsel ifadeleri toplama işlemi şeklinde yazınız.
Cevap:
Cebir karolarının toplamı:
x^2 + 3x + 2
Toplama işlemi şeklinde yazdığınız cebirsel ifade ile çarpma işlemi şeklinde yazdığınız cebirsel ifade arasında nasıl bir ilişki vardır? Açıklayınız.
Cevap:
(x + 2)(x + 1) çarpma ifadesi dikdörtgenin kenarlarının çarpımıyla alanı verir.
x^2 + 3x + 2 ise dikdörtgeni oluşturan karoların alanları toplamıdır.
İki ifade de aynı alanı gösterdiği için birbirine eşittir.
8. Sınıf Matematik Ders Kitabı Sayfa 138. Cevapları Sonuç Yayınları
Alıştırmalar
1. Aşağıdaki basit cebirsel ifadelerin her birini iki farklı biçimde yazınız.
Cevap:
a) −40x²y²
- 1. biçim: −40 · x² · y²
- 2. biçim: −8 · 5 · x²y²
b) 16xy
- 1. biçim: 16 · x · y
- 2. biçim: 8 · 2xy
c) −30a²b
- 1. biçim: −30 · a² · b
- 2. biçim: −6 · 5a²b
ç) 100a²
- 1. biçim: 100 · a²
- 2. biçim: 10 · 10a²
d) 7x + 3
- 1. biçim: (7x) + 3
- 2. biçim: 1 · (7x + 3)
e) 10xy²
- 1. biçim: 10 · x · y²
- 2. biçim: 5 · 2xy²
f) −c²d
- 1. biçim: −1 · c² · d
- 2. biçim: −c · cd
g) 32xyz²
- 1. biçim: 32 · x · y · z²
- 2. biçim: 8 · 4xyz²
ğ) 70a
- 1. biçim: 70 · a
- 2. biçim: 7 · 10a
h) 36ab
- 1. biçim: 36 · a · b
- 2. biçim: 6 · 6ab
ı) −4e²
- 1. biçim: −4 · e²
- 2. biçim: −2 · 2e²
i) −25ed²
- 1. biçim: −25 · e · d²
- 2. biçim: −5 · 5ed²
2. Seçeneklerde bazı dikdörtgenlerin alanları cebirsel ifadeler ile belirtilmiştir. b, c, x, y, a, d ve z pozitif tam sayılar olmak üzere dikdörtgenlerin alabilecekleri kenar uzunluklarını belirleyiniz.
Cevap:
a) Alan = 3bc²
Dikdörtgenin alanı çarpanlara ayrılırsa iki farklı kenar çifti bulunabilir:
• 3bc ve c
• 3b ve c²
b) Alan = 20xy²
Olası kenarlar:
• 4x ve 5y²
• 10y ve 2xy
c) Alan = 30xy²
Olası kenarlar:
• 5y² ve 6x
• 10xy ve 3y
ç) Alan = 15xy
Olası kenarlar:
• 3x ve 5y
• 15 ve xy
d) Alan = 100ad
Olası kenarlar:
• 10a ve 10d
• 25 ve 4ad
e) Alan = 18xyz
Olası kenarlar:
• 6x ve 3yz
• 9xz ve 2y
3. Aşağıda verilen cebirsel ifadelerdeki terimleri, değişkenleri, katsayıları ve sabit terimleri belirleyiniz.
Cevap:
a) 7x² − 4x + 2
- Terimler: 7x², −4x, 2
- Değişken: x
- Katsayılar: 7, −4
- Sabit terim: 2
b) 3ca + a² + 5c − 1
- Terimler: 3ca, a², 5c, −1
- Değişkenler: c, a
- Katsayılar: 3, 1 (a²’nin katsayısı), 5
- Sabit terim: −1
c) 12d − 13 + d²
- Terimler: 12d, −13, d²
- Değişken: d
- Katsayılar: 12, 1 (d²’nin katsayısı)
- Sabit terim: −13

4. Aşağıdaki çarpma işlemlerini yapınız.
Cevap:
a) (x + 2)(x − 5)
= x² − 5x + 2x − 10
= x² − 3x − 10
b) (y − 6)(y − 1)
= y² − y − 6y + 6
= y² − 7y + 6
c) (2z − 2)(2z + 3)
= 4z² + 6z − 4z − 6
= 4z² + 2z − 6
ç) (a + 8)(−1 − a)
= −a − a² − 8 − 8a
= −a² − 9a − 8
d) (−2b + 4)(3b − 2)
= −6b² + 4b + 12b − 8
= −6b² + 16b − 8
e) −7c(−c + 1)
= 7c² − 7c
f) (4 − d)(−2d + 7)
= −8d + 28 + 2d² − 7d
= 2d² − 15d + 28
g) 13e(e − 13)
= 13e² − 169e
ğ) (5k − 1)(−k − 5)
= −5k² − 25k + k + 5
= −5k² − 24k + 5
8. Sınıf Matematik Ders Kitabı Sayfa 139. Cevapları Sonuç Yayınları
5) Şemalarda belirtilen işlemleri yaparak boş kutucuklara yazılması gereken cebirsel ifadeleri belirleyiniz.
Cevap:
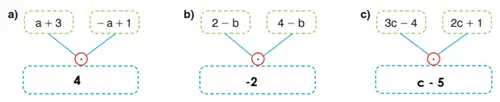
a) (a + 3) + (-a + 1)
İşlem:
(a + 3) + (-a + 1)
Benzer terimleri toplayalım:
a + (-a) = 0
3 + 1 = 4
b) (2 – b) – (4 – b)
İşlem:
(2 – b) – (4 – b)
İkinci ifadenin işaretleri değişir:
2 – b – 4 + b
Benzer terimleri toplayalım:
-b + b = 0
2 – 4 = -2
c) (3c – 4) – (2c + 1)
İşlem:
(3c – 4) – (2c + 1)
İkinci ifadenin işaretleri değişir:
3c – 4 – 2c – 1
Benzer terimleri toplayalım:
3c – 2c = c
-4 – 1 = -5
6) Aşağıdaki cebir karolarının içlerine alanları yazılmıştır. Aynı renkli cebir karoları eş olduğuna göre cebir karolarıyla modellenen çarpma işlemlerini yazınız.
Cevap:
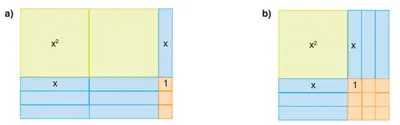
a) Model
Üst kenar: x + 1
Yan kenar: x + 2
Çarpma işlemi: (x + 2)(x + 1)
b) Model
Üst kenar: 3x
Yan kenar: x + 1
Çarpma işlemi: 3x(x + 1)
7) Yandaki PRST dikdörtgeninde | PR | = (3x -1 )br ve | RS | = (x + 2) br’dir.
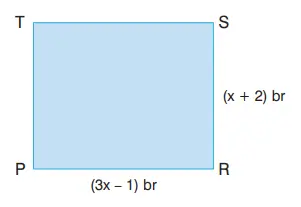
x, 1 ’den büyük pozitif bir tam sayı olduğuna göre PRST dikdörtgeninin alanını belirten cebirsel ifadeyi yazınız.
Cevap:
Alan = |PR| · |RS|
= (3x − 1)(x + 2) br²
Açarsak:
(3x − 1)(x + 2) = 3x² + 6x − x − 2
= 3x² + 5x − 2 br²
Sonuç: (3x − 1)(x + 2) veya 3x² + 5x − 2 br²