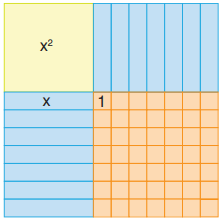8. Sınıf Matematik Ders Kitabı Sayfa 140-147. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 140-147. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 140-141-142-143-144-145-146-147 konularına ait cevapları bulabilirsiniz. “Özdeşlikler Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 140-147. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Özdeşlikler Etkinlik Cevapları
3. Ünite Cebirsel İfadeler ve Özdeşlikler: Cebirsel ifadelerde özdeşlikler, değişkenin her değeri için doğru olan eşitliklerdir. Karenin alanı gibi geometrik şekillerin alan formüllerinde de özdeşlikler kullanılarak hesaplamalar kolayca yapılabilir.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 140. Cevapları Sonuç Yayınları
Ankara ili, Nallıhan ilçesi sınırları içerisinde yer alan ve tarihî ipek yolu üzerinde olan Nallıhan Kuş Cenneti’nde kara leylek, kızıl şahin, kukumav, kaya kırlangıcı, kaya sıvacı ve birçok kuş türü bulunmaktadır. Nallıhan Kuş Cenneti’ndeki kuş sayısının 2 fazlasının 3 katı ile 3 katının 6 fazlası aynı olabilir mi? Açıklayınız
Cevap:
Kuş sayısı x olsun.
Kuş sayısının 2 fazlasının 3 katı: 3(x + 2)
Kuş sayısının 3 katının 6 fazlası: 3x + 6
Aynı olabilir mi diye iki ifadeyi eşitleyelim: 3(x + 2) = 3x + 6
Dağıtalım: 3x + 6 = 3x + 6
Bu eşitlik her zaman doğrudur. Yani x hangi değer olursa olsun iki ifade birbirine eşittir.
Sonuç: Evet, aynı olabilir. Hatta her zaman aynıdır, çünkü iki ifade de aynı sonucu verir.
8. Sınıf Matematik Ders Kitabı Sayfa 140. Cevapları Sonuç Yayınları
Alıştırmalar
1. Aşağıdaki eşitlikler özdeşlik ise ilgili kutucuğa “Ö”, değil ise “D” yazınız.
Cevap:
a) 7·(x−2) = 7x−14 → Ö. Dağılım ile sağlanır (7x−14 = 7x−14).
b) (x−3)² = x² + 6x + 9 → D. Çünkü (x−3)² açıldığında x² − 6x + 9 olur; sağdaki +6x hatalı.
c) (x+6)² = x² + 12x + 36 → Ö. Açınca x²+12x+36 elde edilir.
ç) x² − 2y² = (x−2y)(x+2y) → D. (x−2y)(x+2y) = x² − (2y)² = x² − 4y², sağ ifadeden farklı.
2. Aşağıda modellenen özdeşlikleri yazınız.
Cevap:
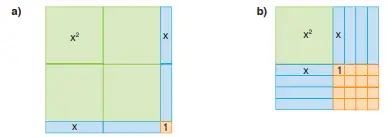
a) Modelin gösterdiği alan özdeşliği:
Modelde 1 tane x² karesi, 2 tane x dikdörtgeni ve 1 tane 1’lik kare vardır.
Bu nedenle toplam alan: x² + 2x + 1
Bu model, kenar uzunluğu (x + 1) olan bir kareyi temsil eder.
Bu yüzden: (x + 1)² = x² + 2x + 1
b) Modelin gösterdiği alan özdeşliği:
Modelde 1 tane x² karesi, 5 tane x dikdörtgeni ve 4 tane 1’lik kare vardır.
Bu nedenle toplam alan: x² + 5x + 4
Bu model, kenar uzunlukları (x + 4) ve (x + 1) olan bir dikdörtgendir.
Bu yüzden: (x + 4)(x + 1) = x² + 5x + 4
3. Aşağıdaki noktalı yerlere uygun cebirsel ifadeleri yazarak özdeşlikler oluşturunuz.
Cevap:
a) (-x + 5y)² = x² − 10xy + 25y²
b) (x + 4y)² = x² + 8xy + 16y²
c) (4x − 2y)² = 16x² − 16xy + 4y²
ç) 49x² − y² = (7x − y)(7x + y)
d) x² − 4y² = (x − 2y)(x + 2y)
e) 100x² − 100y² = 100(x − y)(x + y)
4. Bir karenin kenar uzunluğu (a + 5) br’dir. a pozitif bir sayı olmak üzere karenin alanını belirten özdeşliği yazınız.
Cevap: (a + 5)^2 = a^2 + 10a + 25
Sonraki Ödevler
