8. Sınıf Matematik Ders Kitabı Sayfa 148-153. Cevapları

8. Sınıf Matematik Ders Kitabı Sayfa 148-153. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 148-149-150-151-152-153 konularına ait cevapları bulabilirsiniz. “Cebirsel İfadeleri Çarpanlara Ayırma Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 148-153. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.

Cebirsel İfadeleri Çarpanlara Ayırma Cevapları

3. Ünite Cebirsel İfadeler ve Özdeşlikler: Cebirsel ifadelerin çarpanlarına ayırma işlemi, ifadelerin daha basit çarpımlara ayrılmasını sağlar. Bu işlem, özellikle kareler ve kareler farkı için kullanılan özel çarpım formülleriyle kolayca yapılabilir.

8. Sınıf Matematik Ders Kitabı Sayfa 148. Cevapları Sonuç Yayınları

Çağdaş Bey, odasında bulunan kare şeklindeki aynaya bakarken aynanın bir yüzünün alanını (x + 8)² m² olarak belirtiyor. Buna göre aynanın bir kenar uzunluğu metre biriminde belirtilirken nasıl bir yol izlenmelidir? Açıklayınız.
Cevap:
Ayna kare olduğu için alan = kenar²’dir.
Alan (𝑥+8)² olduğuna göre, karekök alınır.
Bu nedenle aynanın bir kenar uzunluğu 𝑥+8 metredir.

8. Sınıf Matematik Ders Kitabı Sayfa 153. Cevapları Sonuç Yayınları

Alıştırmalar

1) Aşağıdaki cebirsel ifadeleri çarpanlara ayırınız.
Cevap:

a)
7x² + 28x + 28 = 7(x² + 4x + 4) = 7(x + 2)²

b)
128 − 16a² = 16(8 − a²) = 16(√8 − a)(√8 + a)

c)
9c² + 18c + 9 = 9(c² + 2c + 1) = 9(c + 1)²

ç)
16e² − 361 = (4e)² − 19² = (4e − 19)(4e + 19)

d)
196 − 25x² = 14² − (5x)² = (14 − 5x)(14 + 5x)

e)
121a² − 49b² = (11a)² − (7b)² = (11a − 7b)(11a + 7b)

f)
900x² − 1 = (30x)² − 1² = (30x − 1)(30x + 1)

g)
d² + 40d + 400 = d² + 2·20·d + 20² = (d + 20)²

ğ)
a² − 2a + 1 = (a − 1)²

h)
y² + 26y + 169 = y² + 2·13·y + 13² = (y + 13)²

ı)
c² − 30c + 225 = c² − 2·15·c + 15² = (c − 15)²

i)
x² + 12x + 36 = (x + 6)²

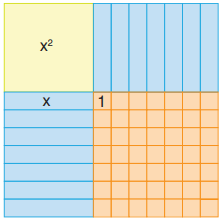
2) Cebir karolarıyla yanda modellenen çarpanlara ayırma işlemini yazınız.
Cevap:
Modelde
1 tane x²,
14 tane x,
49 tane birim kare vardır.

Bu nedenle cebirsel ifade:
x² + 14x + 49

Bu ifade çarpanlara ayrılırsa:
(x + 7)(x + 7)

Sonuç: (x + 7)²

3) x² − 25 ile x² − △x + 25 cebirsel ifadelerinin birer çarpanları ortaktır. Buna göre △ yerine hangi pozitif tam sayı yazılmalıdır?
Cevap:
x² − 25 ifadesi iki kare farkıdır:
x² − 25 = (x − 5)(x + 5)

x² − △x + 25 ifadesinin bir çarpanı ortak olmalıdır.
Bu nedenle (x − 5)² şeklinde yazılır.

(x − 5)² = x² − 10x + 25

Buradan △ = 10 bulunur.

4) a = √7 + 12 olduğuna göre a² − 24a + 144 cebirsel ifadesinin değerini bulunuz.
Cevap:
Verilen:
a = √7 + 12

İfade düzenlenirse:
a² − 24a + 144 = (a − 12)²

Yerine yazılır:
(a − 12)² = (√7)²

Sonuç: 7

Sonraki Ödevler

Sonraki ödevinizi aşağıdaki aramadan bulabilirsiniz.