8. Sınıf Matematik Ders Kitabı Sayfa 159-160-161-162. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 159-160-161-162. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 159-160-161-162 konularına ait cevapları bulabilirsiniz. “3. Ünite Değerlendirme Soruları Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 159-160-161-162. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
3. Ünite Değerlendirme Soruları Etkinlik Cevapları -2
3. Ünite Cebirsel İfadeler ve Özdeşlikler: Olasılık hesaplamalarında, olasılıkların eşit olması ve olası durumların doğru şekilde belirlenmesi önemlidir. Geometrik şekillerle ilgili problemlerde ise alan ve çevre hesaplamaları, cebirsel ifadelerin düzenlenmesiyle çözülür.
Önceki Sayfalar: 154-155-156-157-158
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 159. Cevapları Sonuç Yayınları

21) Görseldeki A, B ve C kutularında renkleri dışında özdeş olan sarı ve mavi toplar bulunmaktadır.
• Toplam sarı top sayısı 6’dır.
• Toplam mavi top sayısı 24’tür.
• Her bir kutudaki sarı top sayısı birbirinden farklıdır.
• Her bir kutudan seçilen bir topun sarı olma olasılığı birbirine eşittir.
Buna göre kutulardan herhangi birinde bulunan mavi top sayısı aşağıdakilerden hangisi olamaz?
Cevap: D) 16
Toplam 6 sarı top vardır ve her kutuda farklı olduğuna göre sarı toplar
1, 2 ve 3 şeklinde dağılır.
Sarı top seçilme olasılıkları eşit olduğundan sarı ve mavi toplar orantılıdır.

Yani 1 sarı topa 4 mavi top düşer.
Buna göre mavi toplar:
4, 8 ve 12 olabilir. 16 olamaz.
22) Ayrıt uzunlukları farklı iki küp aşağıdaki gibi üst üste yerleştirilmiştir.
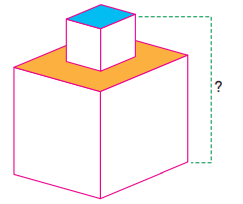
Sonra üst yüzler görseldeki gibi boyanmıştır.
Mavi boyalı alan (4×2 + 12x + 9) birimkare,
Turuncu boyalı alan (5×2-6x-8) birimkaredir.
Buna göre yapının yüksekliğinin x türünden eşiti aşağıdakilerden hangisidir?
Cevap: B) 5x + 4
Mavi alan küçük küpün üst yüzüdür.
4x² + 12x + 9
= (2x + 3)²
→ Küçük küpün bir ayrıtı 2x + 3 tür.
Turuncu alan, büyük küpün üst yüzeyinden küçük küpün tabanı çıkarılarak elde edilmiştir.
Büyük küpün bir ayrıtı a olsun.
a² − (4x² + 12x + 9) = 5x² − 6x − 8
a² = 9x² + 6x + 1
a² = (3x + 1)²
→ Büyük küpün bir ayrıtı 3x + 1 dir.
Toplam yükseklik:
(2x + 3) + (3x + 1)
= 5x + 4
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 160. Cevapları Sonuç Yayınları
23) Aşağıda verilen yapı, 5 özdeş küp kullanılarak oluşturulmuştur.
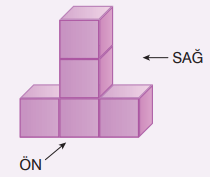
Bu yapıya sağ taraftan bakan birinin gördüğü alan 3ײ + 30x + 75 cm² dir.
Buna göre bu yapıya önden bakıldığında görünen şeklin çevre uzunluğu cm cinsinden aşağıdakilerden hangisi ile ifade edilir?
Cevap: C)12x + 60
Sağdan görülen alan:
3x² + 30x + 75
= 3(x + 5)²
Bir küpün ayrıtı: x + 5
Önden görünüm:
yükseklik = 3a, genişlik = 2a
Çevre = 2(3a + 2a) = 10a
= 10(x + 5)
= 12x + 60
24) Aşağıda mavi, turuncu ve beyaz renkli kare biçimindeki üç karton üst üste yerleştirilmiştir.

- En alttaki mavi kartonun bir kenar uzunluğu, turuncu kartonun bir kenar uzunluğundan 3 cm fazladır.
- En üstteki beyaz kartonun bir kenar uzunluğu, turuncu kartonun bir kenar uzunluğundan x cm eksiktir.
Mavi kartonun alanı (9ײ + 12x + 4) cm² olduğuna göre son durumda mavi kartonun görünen kısmının alanı kaç santimetrekaredir?
Cevap: C) 6x + 18
Mavi karton alanı:
9x² + 12x + 4 = (3x + 2)²
Mavi kenar: 3x + 2
Turuncu kenar: 3x − 1
Beyaz kenar: 2x − 1
Görünen mavi alan:
(3x + 2)² − (2x − 1)²
= 6x + 18
8. Sınıf Matematik Ders Kitabı Sayfa 161. Cevapları Sonuç Yayınları
25) 1 ve 2. kutularda özdeş kırmızı ve beyaz renkli toplar vardır. 1. kutunun içinde kaç top olduğu bilinmezken 2. kutuda 5 adet kırmızı 1 adet beyaz top vardır.
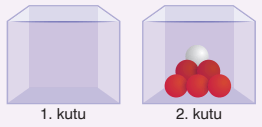
1. kutunun içinden rastgele bir top alındığında alınan bu topun renginin kırmızı olma olasılığının 2/3 olduğu bilinmektedir.
1. kutuda bulunan tüm toplar 2. kutuya konulduktan sonra 2. kutudan rastgele alınan bir topun beyaz renkli olma olasılığı 1/4 olmaktadır.
Buna göre iki kutuda toplam kaç adet top vardır?
Cevap: B) 12
- kutuda kırmızı olma olasılığı 2/3 olduğuna göre
kırmızı = 2k, beyaz = k - kutuda: 5 kırmızı, 1 beyaz
Tüm toplar 2. kutuya konulduktan sonra beyaz olma olasılığı 1/4’tür.
(k + 1) / (3k + 6) = 1 / 4
4k + 4 = 3k + 6
k = 2
Toplam top sayısı = 6 + 6 = 12
26) Kısa kenar uzunlukları 3 birim olan ABCD dikdörtgeni ile EFGH dikdörtgeninin alanları sırası ile (3a + 6) br2 ve (6a + 18) br2 dir.
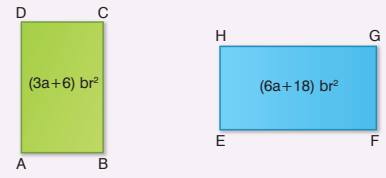
Bu iki dikdörtgen eş kenarlarından uç uca birleştirilerek yeni bir dikdörtgen elde ediliyor. Buna göre elde edilen dikdörtgenin çevre uzunluğu kaç birim olur?
Cevap: A) 6a + 22
Kısa kenar = 3
- dikdörtgen uzun kenar:
(3a + 6) / 3 = a + 2 - dikdörtgen uzun kenar:
(6a + 18) / 3 = 2a + 6
Uç uca birleşince uzun kenar:
(a + 2) + (2a + 6) = 3a + 8
Çevre = 2(3 + 3a + 8)
Çevre = 6a + 22
8. Sınıf Matematik Ders Kitabı Sayfa 162. Cevapları Sonuç Yayınları
27) Mete, aşağıdaki şekilde verilen harf ve rakamlarla ilk hanesi harf, diğer iki hanesi rakam olacak biçimde üç haneli şifreler oluşturacaktır.
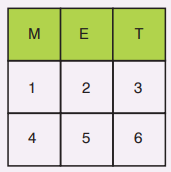
Oluşturulacak şifrelerdeki 2. rakam 1. rakamın bulunduğu kareye ortak kenarı olmayan karelerin birinden seçilecektir.
Örneğin ilk hane M harfi, 2. hane 2 seçilirse 3. hanedeki rakam 2’nin yazılı olduğu kareye ortak kenarı olmayan karelerdeki 4 veya 6 rakamından biri olabilir.
Mete verilen kurala göre oluşturduğu her bir şifreyi ayrı kartlara yazıp bir torbaya atıyor.
Bu torbadan rastgele bir kart seçildiğinde kartın üzerindeki şifrenin son iki rakamının bir tam kare sayı olma olasılığı kaçtır?
Cevap: C) 1/8
Her harf için 16 şifre vardır.
Toplam durum: 3 × 16 = 48
Tam kare olabilecek sayılar: 16, 25, 36, 64
Kuralı sağlayanlar: 16 ve 64 (2 tane)
İstenen durum: 2 × 3 = 6
Olasılık = 6 / 48 = 1 / 8
28) Ahmet, Ali’ye okuduğu kitabın kaç sayfalık bir kitap olduğunu sorduğunda Ali, Ahmet’e “Benim okuduğum kitaptan rastgele bir sayfa açtığında bu sayfa numarasının 3’ün pozitif tam sayı kuvveti olma olasılığı ile 4’ün pozitif tam sayı kuvveti olma olasılıkları eşittir. Aynı zamanda benim okuduğum kitap 100 sayfadan az, olabilecek en fazla sayfaya sahiptir.” demiştir.
Buna göre Ali’nin kitabı kaç sayfadır?
Cevap: B) 65
100’den küçük
3’ün kuvvetleri: 3, 9, 27, 81
4’ün kuvvetleri: 4, 16, 64
Olasılıkların eşit olması için kitapta bu sayıların sayısı eşit olmalıdır.
Bu durum 64’e kadar sağlanır.
100’den küçük en büyük sayfa sayısı: 65
Önceki Sayfalar: 154-155-156-157-158