8. Sınıf Matematik Ders Kitabı Sayfa 164-169. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 164-169. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 164-165-166-167-168-169 konularına ait cevapları bulabilirsiniz. “Birinci Dereceden Bir Bilinmeyenli Denklemler Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 164-169. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Birinci Dereceden Bir Bilinmeyenli Denklemler Cevapları
4. Ünite doğrusal Denklemler: Birinci dereceden denklemler, bilinmeyen değeri yalnız bırakılarak basit adımlarla çözülür. Bu denklemler günlük yaşam problemlerini modellemede ve geometrik hesaplamalarda sıkça kullanılır.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 164. Cevapları Sonuç Yayınları
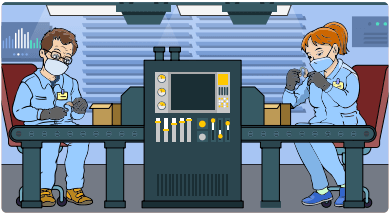
Furkan Bey ile Esin Hanım görseldeki atölyede birlikte çalışmaktadır. Furkan Bey, Esin Hanım’ın ürettiği işitme cihazı sayısının 2 katının 20 eksiği kadar işitme cihazı üretmiştir. Furkan Bey, atölyede 24 adet işitme cihazı ürettiğine göre Esin Hanım’ın atölyede ürettiği işitme cihazı sayısı bulunurken nasıl bir yol izlenmelidir? Açıklayınız.
Cevap:
Adım 1: Eşitliğin her iki tarafına 20 ekleyelim (eksi 20’yi yok etmek için):
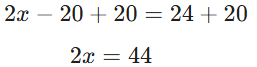
Adım 2: x değerini yalnız bırakmak için her iki tarafı 2’ye bölelim:
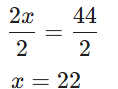
Esin Hanım atölyede 22 adet işitme cihazı üretmiştir.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 169. Cevapları Sonuç Yayınları
Alıştırmalar
1) Aşağıdaki birinci dereceden bir bilinmeyenli denklemleri çözerek denklemlerdeki x değerlerini bulunuz.
Cevap: Bu soruda temel amaç, payda eşitleyerek veya içler dışlar çarpımı yaparak x değerini yalnız bırakmaktır.

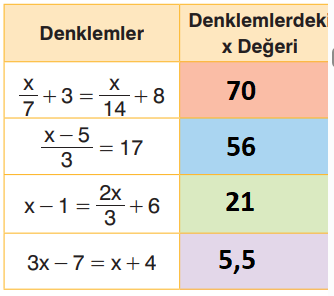
2) Yandaki tabloda, birinci dereceden bir bilinmeyenli denklemler verilmiştir. Denklemleri çözerek tablodaki renkli bölgelere x değerini yazınız.
Cevap: Her bir denklemde hedefimiz, bilinmeyen olan x değerini eşitliğin bir tarafında yalnız bırakmaktır.

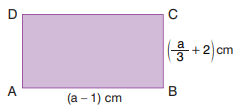
3) Yandaki ABCD dikdörtgeninde | AB | = (a -1) cm ve | BC | = (a/3+2) cm’dir. ABCD dikdörtgeninin çevre uzunluğu 26 cm olduğuna göre | CD | kaç cm’dir?
Cevap:
Verilenler:
AB = a − 1
BC = a/3 + 2
Çevre = 26 cm
Denklem:
2[(a − 1) + (a/3 + 2)] = 26
Çözüm:
(a − 1) + (a/3 + 2) = a + a/3 + 1
2(a + a/3 + 1) = 26
a + a/3 + 1 = 13
a + a/3 = 12
3a + a = 36
4a = 36
a = 9
Sonuç:
CD = AB = a − 1 = 8 cm

4) Avukat Esma Hanım’ın aldığı dava için çalıştığı sürenin çeyreğinin 13 dakika fazlası 113 dakikadır. Buna göre Esma Hanım aldığı dava için kaç dakika çalışmıştır?
Cevap:
Çalışma süresinin çeyreğinin 13 fazlası 113 dakika.
Denklem:
x/4 + 13 = 113
13 çıkarılır:
x/4 = 100
4 ile çarpılır:
x = 400
Esma Hanım aldığı dava için 400 dakika çalışmıştır.