8. Sınıf Matematik Ders Kitabı Sayfa 178-182. Cevapları

8. Sınıf Matematik Ders Kitabı Sayfa 178-182. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 178-179-180-181-182 konularına ait cevapları bulabilirsiniz. “Doğrusal Denklemlerin Grafiği Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 178-182. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.

Doğrusal Denklemlerin Grafiği Cevapları

4. Ünite doğrusal Denklemler: Doğrusal denklemler, koordinat düzleminde bir doğru olarak ifade edilir ve bu doğrular eksenlere paralel, orijinden geçen veya eksenleri kesen özellikler gösterebilir. Doğrunun denklemi, bu grafiksel özellikleri belirlemek için kullanılır.

İçindekiler

8. Sınıf Matematik Ders Kitabı Sayfa 178. Cevapları Sonuç Yayınları

8. Sınıf Matematik Ders Kitabı Sayfa 178. Cevapları

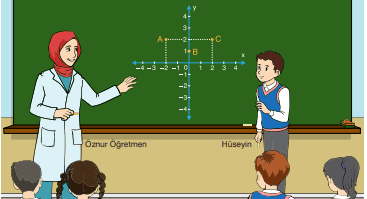
Öznur Öğretmen, tahtaya bir koordinat sistemi çizmiş ve koordinat sisteminde A, B ve C noktalarını görseldeki gibi göstermiştir. Öznur Öğretmen, Hüseyin’e “Koordinat sistemindeki A, B ve C noktalarını birleştirerek bir doğru elde edebilir misin? Elde edemezsen B noktasında nasıl bir değişiklik yapman gerekir?” sorusunu sormuştur.
Hüseyin, Öznur Öğretmen’e nasıl bir cevap vermelidir? Açıklayınız.
Cevap:
A ve C noktaları y = 2 doğrusu üzerindedir.
B noktası bu doğru üzerinde değildir.
Bu nedenle üç nokta birleştirilerek doğru elde edilemez.
B noktası (0, 2) yapılırsa y = 2 doğrusu elde edilir.

Farklı bir sayfa mı arıyorsunuz?

İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:

MEB Yayınları SONUÇ Yayıncılık Tüm Kitaplar

8. Sınıf Matematik Ders Kitabı Sayfa 182. Cevapları Sonuç Yayınları

Alıştırmalar

1) Aşağıda denklemleri verilen doğruların grafiklerini koordinat sisteminde çiziniz. Doğru grafiklerinin eksenlere paralel olup olmadığını belirleyiniz.
Cevap:
a) x = −1
x değeri her zaman −1’dir.
Örnek noktalar:
(−1, −2), (−1, 0), (−1, 2)
→ y eksenine paralel doğru

b) x = 3
x değeri her zaman 3’tür.
Örnek noktalar:
(3, −2), (3, 0), (3, 2)
→ y eksenine paralel doğru

c) y = −2
y değeri her zaman −2’dir.
Örnek noktalar:
(−2, −2), (0, −2), (2, −2)
→ x eksenine paralel doğru

ç) y = 4
y değeri her zaman 4’tür.
Örnek noktalar:
(−2, 4), (0, 4), (2, 4)
→ x eksenine paralel doğru
8. Sınıf Matematik Ders Kitabı Sayfa 182. Cevapları
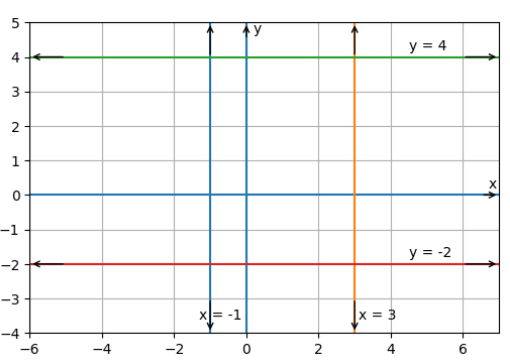
x = −1 ve x = 3 doğruları y eksenine paraleldir.
y = −2 ve y = 4 doğruları x eksenine paraleldir.

2) Aşağıda denklemleri verilen doğruların grafiklerini koordinat sisteminde çiziniz. Doğru grafiklerinin orijinden geçip geçmediğini belirleyiniz.
Cevap:
a) y = −2x

x = 0 ⇒ y = 0 → (0, 0)
x = 1 ⇒ y = −2 → (1, −2)

b) y = −x / 5

x = 0 ⇒ y = 0 → (0, 0)
x = 5 ⇒ y = −1 → (5, −1)

c) y = x / 3

x = 0 ⇒ y = 0 → (0, 0)
x = 3 ⇒ y = 1 → (3, 1)

ç) y = x

x = 0 ⇒ y = 0 → (0, 0)
x = 2 ⇒ y = 2 → (2, 2)

8. Sınıf Matematik Ders Kitabı Sayfa 182. Cevapları
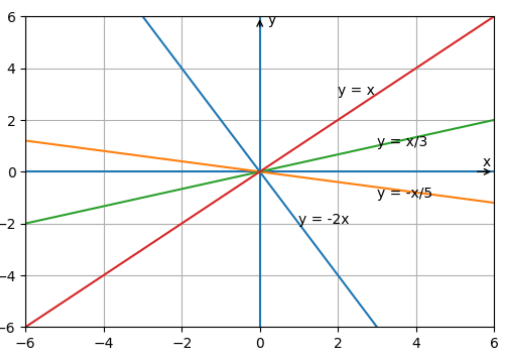
y = −2x, y = −x/5, y = x/3 ve y = x doğrularında x = 0 iken y = 0 olur.
Bu nedenle tüm doğrular orijinden geçmektedir.

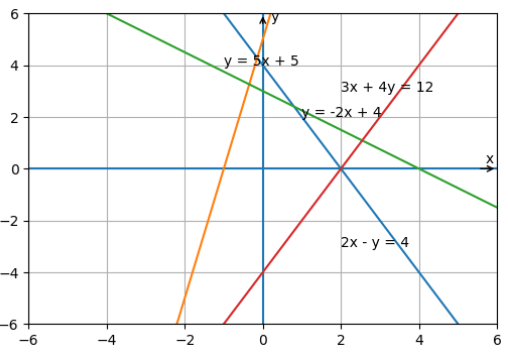
3) Aşağıda denklemleri verilen doğruların grafiklerini koordinat sisteminde çiziniz. Doğru grafiklerinin eksenleri kestiği noktaları belirleyiniz.
Cevap:

a) y = −2x + 4