8. Sınıf Matematik Ders Kitabı Sayfa 250-255-258-259. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 250-255-258-259. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 250-251-252-253-254-255-256-257-258-259 konularına ait cevapları bulabilirsiniz. “Pisagor Bağıntısı Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 250-255-258-259. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Pisagor Bağıntısı Cevapları
5. Ünite Üçgenler: Pisagor bağıntısı, dik üçgenlerin kenar uzunlukları arasında a² + b² = c² ilişkisi kurar. Bu bağıntı, geometrik problemlerde ve iki nokta arasındaki mesafeyi bulmada kullanılır.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 250. Cevapları Sonuç Yayınları
MÖ 570 ile 495 yılları arasında yaşayan Pisagor, matematik alanında birçok çalışma ve eser ortaya koymuştur.
Sayıların filozofu olarak bilinen Pisagor, her şeyin sayılarla ilişkili olduğunu belirtmiştir. Pisagor, üçgenlerin bilinmeyen kenar uzunluklarının bilinen kenar uzunluklarından faydalanarak bulunmasına yönelik bir bağıntı oluşturmuştur. Üçgenlerin kenar uzunluklarını bulmaya yönelik çalışmalar yapan diğer bilim insanlarını araştırınız.
Cevap:
Üçgenlerin kenar uzunluklarıyla ilgili çalışmalar yapan bilim insanlarından bazıları Öklid ve El-Harezmi’dir.
Öklid, üçgenlerin kenar ve açı ilişkilerini incelemiştir.
El-Harezmi ise cebirsel yöntemlerle geometrik problemleri çözmüştür.
Etkinlik
Araç Gereçler: A4 kâğıdı, kareli kâğıt, makas, pembe, mavi, sarı ve turuncu boya kalemleri.
Kareli kâğıda, alanları sırasıyla 25 cm2,16 cm2 ve 9 cm2 olan üç farklı kare çiziniz.
Cevap:
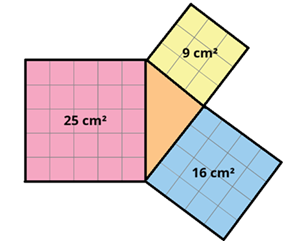
Kareleri sırasıyla pembe, mavi ve sarıya yandaki gibi boyayınız.
Pembe, mavi ve sarı kareleri, makas kullanarak kesiniz (Makas kullanırken dikkatli olunuz.).
Pembe, mavi ve sarı karelerin kenarlarını yandaki gibi kullanarak A4 kâğıdının üzerine yerleştiriniz. Kenarlarla oluşturduğunuz üçgeni yandaki gibi turuncuya boyayınız. Turuncu üçgen, bir dik üçgen olabilir mi? Açıklayınız.
Cevap:
Turuncu üçgen bir dik üçgendir.
Çünkü karelerin kenar uzunlukları 3 cm, 4 cm ve 5 cm olup 3² + 4² = 5² olduğundan Pisagor bağıntısı sağlanmaktadır.
Kareli kâğıda alanları sırasıyla 49 cm2, 36 cm2 ve 9 cm2 olan üç farklı kare çiziniz.
Cevap:
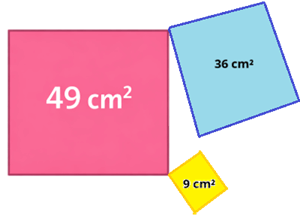
Kareleri sırasıyla pembe, mavi ve sarıya boyayınız.
Pembe, mavi ve sarı kareleri, makas kullanarak kesiniz (Makas kullanırken dikkatli olunuz.).
Pembe, mavi ve sarı karelerin kenarlarını kullanarak bir dik üçgen elde edebilir misiniz? Açıklayınız.
Cevap:
Karelerin kenar uzunlukları 7 cm, 6 cm ve 3 cm’dir.
3² + 6² ≠ 7² olduğundan bu karelerle bir dik üçgen oluşturulamaz.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 255. Cevapları Sonuç Yayınları
Problem
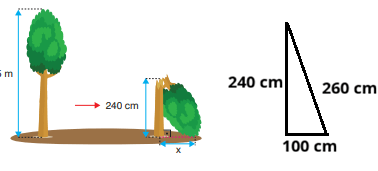
Bir fırtınada zarar gören 5 m uzunluğundaki bir ağacın gövdesi yerden 240 cm yükseklikten kırılmış ve kırılan bölüm gövdeden tam olarak kopmayarak eğik bir şekilde görseldeki gibi toprağa değmiştir.
Buna göre ağacın toprakta olan gövdesi ile kırılarak toprağa değdiği yer arasındaki uzaklık kaç cm’dir?
Cevap:
Ağacın kırılan kısmının uzunluğu 500 − 240 = 260 cm’dir.
260² = 240² + x²
x = 100 cm
Sonuç: 100 cm
8. Sınıf Matematik Ders Kitabı Sayfa 258. Cevapları Sonuç Yayınları
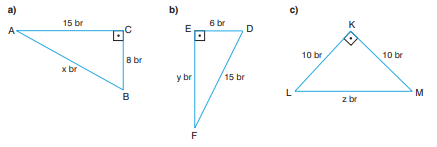
1) Aşağıdaki dik üçgenlerde verilen kenar uzunluklarına göre x, y ve z değerlerini bulunuz.
Cevap:
a)
Dik üçgende Pisagor bağıntısı kullanılır.
15 br ve 8 br dik kenarlardır.
15² + 8² = x²
225 + 64 = x²
289 = x²
x = 17 br
b)
15 br hipotenüstür, 6 br bir dik kenardır.
6² + y² = 15²
36 + y² = 225
y² = 189
y = 3√21 br
c)
Dik üçgende iki kenar eşittir.
10² + 10² = z²
100 + 100 = z²
200 = z²
z = 10√2 br
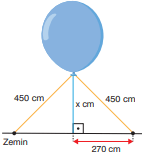
2) Bir firma, reklam balonunu kullanarak tanıtım yapmaya karar vermiştir ve firma, yanda verilen reklam balonunu görseldeki gibi zemine sabitlemiştir. Yanda verilenlere göre reklam balonunun zeminden yüksekliği (x) kaç cm’dir?
Cevap:
Zemindeki 270 cm’lik mesafe ikiye bölünür:
270 ÷ 2 = 135
Dik üçgende Pisagor bağıntısı uygulanır:
450² = x² + 135²
202500 = x² + 18225
x² = 184275
x = 360 cm
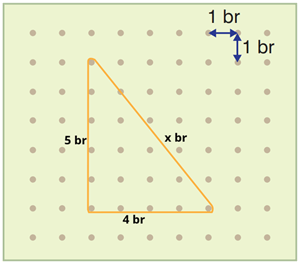
3) Eşref, geometri tahtasında turuncu lastikle yandaki dik üçgen modelini oluşturmuştur. Eşrefin oluşturduğu dik üçgen modelindeki hipotenüsün uzunluğu kaç birimdir?
Cevap:
Dik kenarlar 5 br ve 4 br’dir.
Pisagor’a göre:
x² = 5² + 4² = 41
x = √41 br
8. Sınıf Matematik Ders Kitabı Sayfa 259. Cevapları Sonuç Yayınları
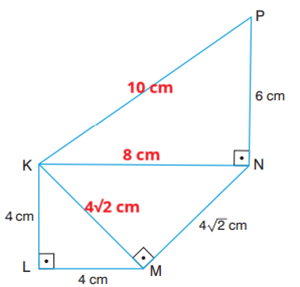
4) Yandaki şekilde KLM, KMN ve KNP, birer dik üçgendir. |MN| = 4y√2 cm, | KL| = |LM| = 4cm, | NP| = 6cm ve | KP | = x cm olduğuna göre x kaçtır?
Cevap: x = 10 cm
Verilenler:
- KL = 4 cm
- LM = 4 cm
- MN = 4√2 cm
- NP = 6 cm
KLM dik üçgeni
KM² = 4² + 4² = 32
KM = 4√2 cm
KMN dik üçgeni
KN² = (4√2)² + (4√2)²
KN² = 32 + 32 = 64
KN = 8 cm
KNP dik üçgeni
KP² = 8² + 6²
KP² = 64 + 36 = 100
KP = 10 cm
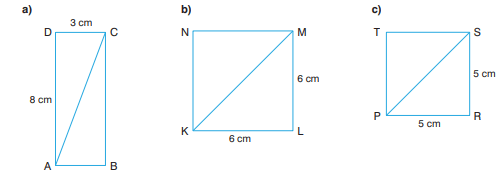
5) Aşağıda kenar uzunlukları verilen dikdörtgen ve karelerin köşegen uzunluklarını bulunuz.
Cevap:
a)
Kenarlar: 3 cm ve 8 cm
Köşegen² = 3² + 8²
Köşegen² = 9 + 64 = 73
Köşegen = √73 cm
b)
Kare (kenar = 6 cm)
Köşegen² = 6² + 6²
Köşegen² = 72
Köşegen = 6√2 cm
c)
Kare (kenar = 5 cm)
Köşegen² = 5² + 5²
Köşegen² = 50
Köşegen = 5√2 cm
6) Koordinat düzleminde A(-2, 3) ile B(0, -1) noktalarının arasındaki uzaklığı bulunuz.
Cevap:
Uzaklık = √[(0 − (−2))² + (−1 − 3)²]
Uzaklık = √[2² + (−4)²]
Uzaklık = √(4 + 16)
Uzaklık = √20 = 2√5
Sonuç: 2√5
7) | KL | = 5 cm, | LM | = 5 cm ve | KM | = 5√2 cm olan bir KLM üçgeninin dik üçgen olup olmadığını belirleyiniz.
Cevap:
Verilenler:
KL = 5 cm
LM = 5 cm
KM = 5√2 cm
Pisagor kontrolü yapılır:
5² + 5² = 25 + 25 = 50
(5√2)² = 50
Eşitlik sağlandığı için KLM üçgeni dik üçgendir.