8. Sınıf Matematik Ders Kitabı Sayfa 29-30-31-32. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 29-30-31-32. Cevapları MEB Yayınları bölümünde, ders kitabı sayfa 29-30-31-32 konularına ait cevapları bulabilirsiniz. “Alıştırmalar Cevapları” ve “Düşünme Zamanı Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 29-30-31-32. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
1. Bölüm: Çarpanlar ve Katlar Alıştırmalar Cevapları
1. Ünite 1. Bölüm Çarpanlar ve Katlar: EBOB ve EKOK konularını, temel alıştırmalardan başlayarak çok katmanlı ve gerçek yaşam problemlerine (sporcu dağıtımı, yardım kolileri, akarsu halatları, metro-tramvay seferleri gibi) doğru genişleterek bu kavramların analizini ve uygulanmasını sağlıyor.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 29 Cevapları MEB Yayınları
1. Aşağıdaki sayı çiftlerinin EBOB ve EKOK’larını bulunuz.
Cevap:
a) 6 ve 9
EBOB(6,9) = 3
EKOK(6,9) = 18
Çarpanlar: 6 = 2·3 , 9 = 3²
b) 12 ve 24
EBOB(12,24) = 12
EKOK(12,24) = 24
Çarpanlar: 12 = 2²·3 , 24 = 2³·3
c) 27 ve 36
EBOB(27,36) = 9
EKOK(27,36) = 108
Çarpanlar: 27 = 3³ , 36 = 2²·3²
ç) 30 ve 43
EBOB(30,43) = 1
EKOK(30,43) = 1290
Çarpanlar: 30 = 2·3·5 , 43 = 43
d) 52 ve 64
EBOB(52,64) = 4
EKOK(52,64) = 832
Çarpanlar: 52 = 2²·13 , 64 = 2⁶
e) 88 ve 144
EBOB(88,144) = 8
EKOK(88,144) = 1584
Çarpanlar: 88 = 2³·11 , 144 = 2⁴·3²
f) 120 ve 150
EBOB(120,150) = 30
EKOK(120,150) = 600
Çarpanlar: 120 = 2³·3·5 , 150 = 2·3·5²
g) 256 ve 512
EBOB(256,512) = 256
EKOK(256,512) = 512
Çarpanlar: 256 = 2⁸ , 512 = 2⁹
2. Kış olimpiyatları için Erzurum’a giden 33 Azerbaycanlı ve 42 Kazakistanlı sporcu bir otele yerleştirilecektir. Aynı ülkeden gelen sporcular aynı odada kalmak şartıyla odalara eşit sayıda dağıtılacaktır.
Buna göre sporcuların tamamını istenen şartlarda otele yerleştirmek için en az kaç oda gereklidir?
Cevap:
Oda başına düşecek eşit sayının her iki ülke sayısını da bölebilmesi gerekir → bu sayıyı en büyük yaparsak oda sayısı en az olur. O halde oda başına düşen en büyük sayı = EBOB(33,42) = 3.
Toplam sporcu = 33 + 42 = 75. Oda sayısı = 75 / 3 = 25 oda.
3. Bir kitabın sayfa sayısı ile ilgili aşağıdaki bilgiler veriliyor.
• Sayfa sayısı 60 ile 100 arasındadır.
• Sayfa sayısının asal çarpanları 2 ve 3’tür.
• Sayfa sayısını oluşturan rakamlar aralarında asaldır.
Buna göre aşağıdaki boşluklara kitabın sayfa sayısı ile ilgili yargılar doğru ise “D”, yanlış ise “Y” yazınız.
Cevap:

İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 30 Cevapları MEB Yayınları
4. Bir yardım organizasyonu için hazırlanan koliler beşerli ve sekizerli gruplandırıldığında her seferinde 1 koli artmaktadır.
Toplam koli sayısının 3 basamaklı bir sayı olduğu bilindiğine göre en az kaç koli hazırlanmıştır?
Cevap: Durum:
N ≡ 1 (mod 5) ve N ≡ 1 (mod 8)
→ N − 1 hem 5’e hem 8’e bölünür → N − 1, 5 ve 8’in ortak katı olmalı.
5 ve 8’in EKOK’u = 40.
En küçük 3 basamaklı N için: N = 1 + 40·k ≥ 100
→ k = ⌈99 / 40⌉ = 3
→ N = 1 + 40·3 = 121
Cevap: 121 koli

5. İçinde eşit miktarda su bulunan iki damacana yanda verilmiştir. Damacanalar özdeş ve her birinin hacmi 19 litredir. Kaplar her seferinde
tam doldurularak 1. damacanadaki su 370 mililitrelik kapla, 2. damacanadaki su ise 500 mililitrelik kapla boşaltılabilmektedir.
Buna göre başlangıçta bir damacanada en fazla kaç litre su bulunmaktadır?
Cevap:
370 mL = 0,37 L, 500 mL = 0,5 L
Aranan miktar 0,37 ve 0,5’in ortak katı olmalı ve 19 L’yi geçmemeli.
0,37 = 37/100 L, 0,5 = 1/2 L
EKOK(37,50) = 1850 (payda 100 olduğundan 18,5 L tam bölünür).
Cevap: 18,5 L

6. Yukarıdaki 180 m ve 150 m’lik iki yolun arasından akarsu geçmektedir. Belediye, bu akarsuyun üzerine eşit aralıklarla ve birbirine paralel çelik halatlar koymak istemektedir.
Her iki yolun da başına ve sonuna halat konulmak şartıyla bu iş için toplam en az kaç halat gerekir? (Halatların kalınlığını dikkate almayınız.)
Cevap:
Aralık = EBOB(180,150) = 30 m
Her yol: uzunluk/aralık + 1 = (180/30 + 1) = 7 halat
İki yol için toplam = 7
Cevap: 7 halat
7. Dikdörtgen şeklindeki bir bahçenin uzun kenarı 240 m ve kısa kenarı 180 m uzunluğundadır. Bu bahçenin kenarlarına köşeleri de dâhil olacak şekilde eşit aralıklarla aydınlatma direği dikilecektir.
Bir direğin fiyatı 300 TL olduğuna göre bu iş için en az kaç TL’ye ihtiyaç vardır?
Cevap:
Aralık = EBOB(240,180) = 60 m
Uzun kenar: 240/60 = 4 aralık → 5 direk
Kısa kenar: 180/60 = 3 aralık → 4 direk
Toplam direk = (5 + 5 + 4 + 4) − 4 köşe = 14
Maliyet = 14 × 300 = 4200 TL
Cevap: 4200 TL
8. Sınıf Matematik Ders Kitabı Sayfa 31 Cevapları MEB Yayınları
8. Aynı güzergah üzerinde hareket eden metro ve tramvaydan, metro 1 saat çalışıp 20 dakika ara vermekte, tramvay ise 1 saat çalışıp 30 dakika ara vermektedir.
Saat 08.00’de birlikte kalkan bu araçlar 2. kez saat kaçta birlikte harekete geçer?
Cevap:
Metro: 60 dk çalış + 20 dk ara → 80 dk döngü
Tramvay: 60 dk çalış + 30 dk ara → 90 dk döngü
Birlikte tekrar kalkış için EKOK(80,90) = 720 dk = 12 saat
08.00 + 12 saat = 20.00
Cevap: 20.00
9. Sadece pandaların yaşadığı uzun kenar uzunluğu 480 m ve kısa kenar uzunluğu 360 m olan hayvanat bahçesinin görseli aşağıda verilmiştir.

Bu hayvanat bahçesi eş karesel bölgelere ayrılarak yeniden düzenlenecektir. Oluşacak bölgelerle ilgili aşağıdaki bilgiler verilmiştir:
İki bölgenin köşesi olacak noktalara bambu filizi, dört bölgenin köşesi olacak noktalara su ve tek bir bölgenin köşesi olacak noktalara ise balık konarak pandaların beslenme ihtiyaçları karşılanacaktır.
Her bir bambu filizi için günlük 500 TL, su için 40 TL ve balık için 200 TL gerektiğine göre bir günde pandalar için toplam en az kaç TL harcanır?
Cevap:
Hayvanat bahçesi 480 m × 360 m, karelere ayrılacak. Kare kenarı = EBOB(480,360) = 120 m
Dört karenin köşesi: (satır+1)×(sütun+1) = (4+1)×(3+1) = 20 köşe
• 4 karenin kesişimi (su): iç nokta = 3×2 = 6 → 6 × 40 = 240 TL
• 2 karenin kesişimi (bambu): kenar içi = (20 − 6 − 4 köşe) = 10 → 10 × 500 = 5000 TL
• 1 karenin köşesi (balık): 4 köşe → 4 × 200 = 800 TL
Toplam = 240 + 5000 + 800 = 6040 TL
Cevap: 6040 TL
10. Yarıçapı r olan çemberin uzunluğu 2πr formülü ile bulunur.

A aracının tekerleklerinin yarıçapı 30 cm ve B aracının tekerleklerinin yarıçapı 36 cm’dir. Şekilde gösterilen biçimde harekete başlayan her iki araç bitiş çizgisine geldiğinde tekerleklerinin tam tur attığı bilinmektedir.
Buna göre başlangıç ile bitiş çizgisi arasındaki mesafe en az kaç metredir? (π = 3 alınız.)
Cevap:
A aracı yarıçap 30 cm → çevre = 2·π·30 = 180 cm (π=3)
B aracı yarıçap 36 cm → çevre = 2·π·36 = 216 cm
Mesafe = EKOK(180,216) = 1080 cm = 10,8 m
Cevap: 10,8 m
8. Sınıf Matematik Ders Kitabı Sayfa 32 Cevapları MEB Yayınları
Düşünme Zamanı
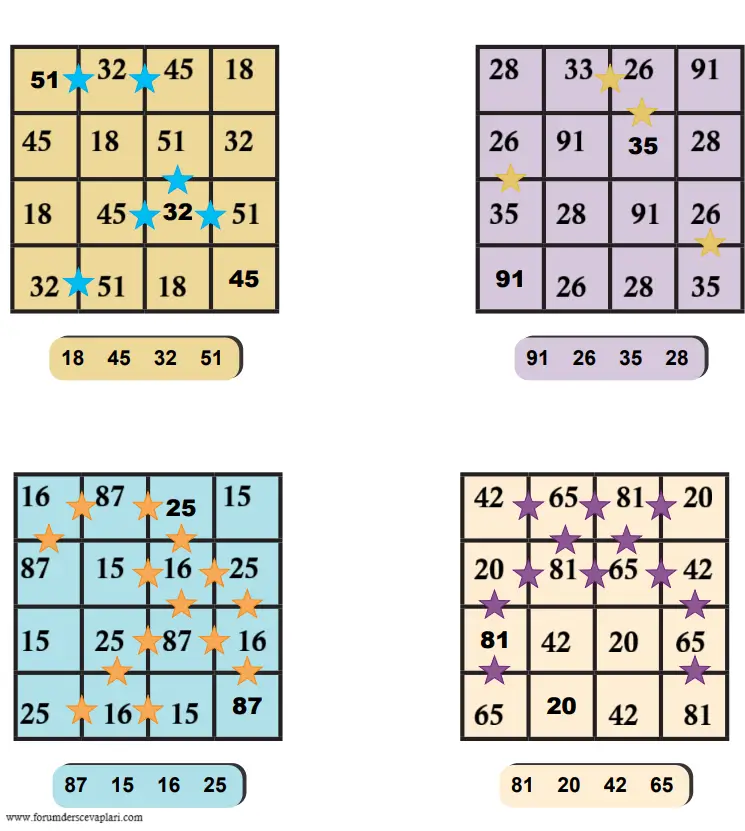
Altlarında verilen dört doğal sayıyı belirtilen kurallara göre yerleştirerek diyagramları doldurunuz.
• Her satır ve sütunda her sayıdan birer tane olmalıdır.
• Aralarında yıldız bulunan komşu hücrelere gelecek iki sayı, aralarında asal olmalıdır.
Cevap: