8. Sınıf Matematik Ders Kitabı Sayfa 42-43-44. Cevapları

8. Sınıf Matematik Ders Kitabı Sayfa 42-43-44. Cevapları MEB Yayınları bölümünde, ders kitabı sayfa 42-43-44 konularına ait cevapları bulabilirsiniz. “Tam Sayıların Tam Sayı Kuvvetleri Alıştırmalar Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 42-43-44. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.

Tam Sayıların Tam Sayı Kuvvetleri Alıştırmalar Cevapları

1. Ünite 2. Bölüm: Üslü İfadeler: Üslü ifadelerin temel kurallarını (çarpma, bölme, kuvvet alma) ve negatif üslerin anlamlarını basitten karmaşığa doğru ilerleyen alıştırmalarla pekiştirerek, bu kuralları karmaşık problemlerde ve strateji gerektiren durumlarda uygulama becerisi kazandırır.

8. Sınıf Matematik Ders Kitabı Sayfa 42 Cevapları MEB Yayınları

1. Aşağıdaki üslü ifadelerin değerlerini bulunuz.
Cevap:

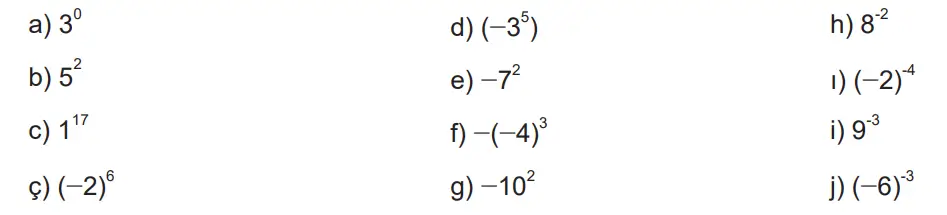
a) 3⁰ = 1

b) 5² = 25

c) 1¹⁷ = 1

ç) (−2)⁶ = 64

d) (−3)⁵ = −243

e) −7² = −49 (parantez olmadığı için önce üs alınır)

f) −(−4)³ = 64

g) −10² = −100

h) 8⁻² = 1/64

ı) (−2)⁻⁴ = 1/16

i) 9⁻³ = 1/729

2. Aşağıdaki işlemlerin sonuçlarını üslü ifade olarak yazınız.
Cevap:

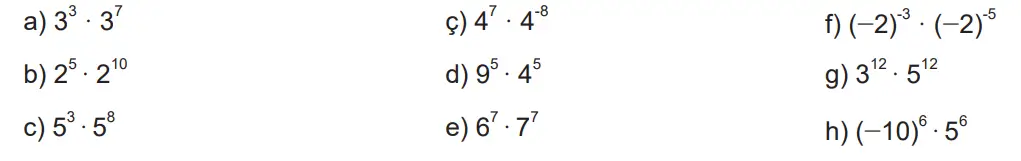
a) 3³ · 3⁷ = 3³⁺⁷ = 3¹⁰

b) 2⁵ · 2¹⁰ = 2¹⁵

c) 5³ · 5⁸ = 5¹¹

ç) 4⁷ · 4⁻⁸ = 4⁻¹

d) 9⁵ · 4⁵ = (9·4)⁵ = 36⁵

e) 6⁷ · 7⁷ = (6·7)⁷ = 42⁷

f) (−2)⁻³ · (−2)⁻⁵ = (−2)⁻⁸

g) 3¹² · 5¹² = (3·5)¹² = 15¹²

h) (−10)⁶ · 5⁶ = (−50)⁶ = 50⁶ (çift kuvvetten dolayı pozitif)

3. Aşağıdaki işlemlerin sonuçlarını üslü ifade olarak yazınız.
Cevap:

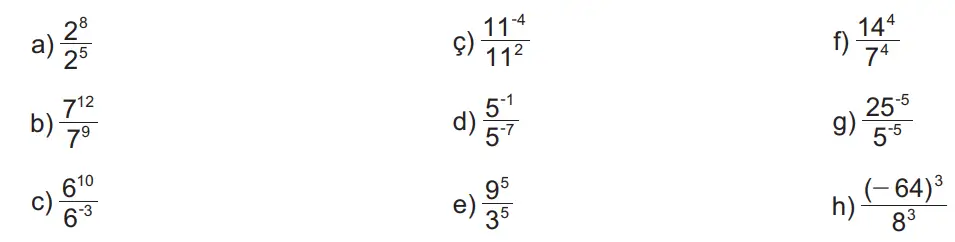
a) 2⁸ ÷ 2⁵ = 2⁸⁻⁵ = 2³

b) 7¹² ÷ 7⁹ = 7³

c) 6¹⁰ ÷ 6⁻³ = 6¹⁰⁻⁽⁻³⁾ = 6¹³

ç) 11⁻⁴ ÷ 11² = 11⁻⁶

d) 5⁻¹ ÷ 5⁻⁷ = 5⁻¹⁻⁽⁻⁷⁾ = 5⁶

e) 9⁵ ÷ 3⁵ = (9÷3)⁵ = 3⁵

f) 14⁴ ÷ 7⁴ = (14÷7)⁴ = 2⁴ = 16

g) 25⁻⁵ ÷ 5⁻⁵ = (25÷5)⁻⁵ = 5⁻⁵

h) (−64)³ ÷ 8³ = (−64÷8)³ = (−8)³ = −512

4. Aşağıdaki işlemlerin sonuçlarını üslü ifade olarak yazınız.
Cevap:

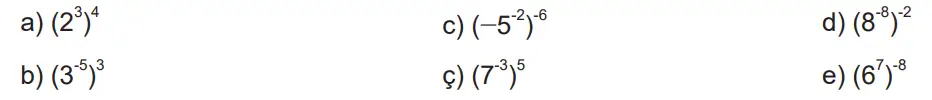
a) (2³)⁴ = 2³·⁴ = 2¹²

b) (3⁻⁵)³ = 3⁻¹⁵

c) (−5²)⁻⁶ = (−25)⁻⁶ = 25⁻⁶

ç) (7⁻³)⁵ = 7⁻¹⁵

d) (8⁻⁸)⁻² = 8¹⁶

e) (6⁷)⁻⁸ = 6⁻⁵⁶

5. 81⁵ · (-729)^-2 · 3⁷ işleminin sonucunun en sade hâlini üslü ifade olarak yazınız.
Cevap:

81 = 3⁴ ve 729 = 3⁶ olduğu için,
(3⁴)⁵ · (-3⁶)⁻² · 3⁷
= 3²⁰ · 3⁻¹² · 3⁷ (Çift kuvvetten dolayı işaret (+) oldu)
= 3²⁰⁻¹²⁺⁷
= 3¹⁵

8. Sınıf Matematik Ders Kitabı Sayfa 43 Cevapları MEB Yayınları

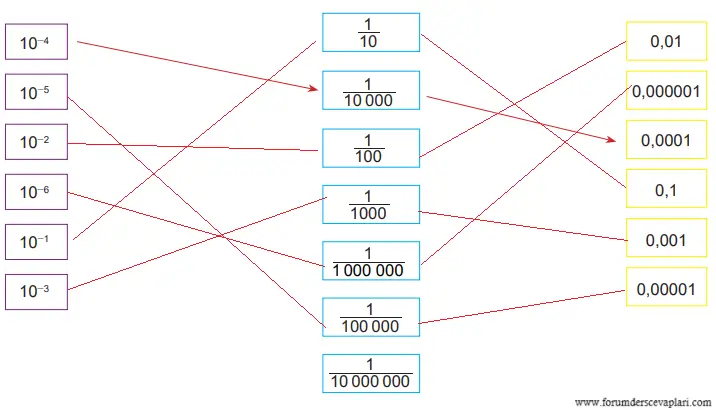
6. Aşağıdaki işlemlerle karşılarındaki ifadeleri bir eşitlik oluşturacak şekilde eşleştiriniz.
Cevap:

a) 2⁻¹² · 4³ = 2⁻¹² · (2²)³ = 2⁻¹² · 2⁶ = 2⁻⁶

b) (−5)⁻² = 1/(−5)² = 1/25 = 5⁻²

c) 3⁷ · (−4)⁷ = (3 · (−4))⁷ = (−12)⁷

ç) 2⁻² · (2⁷ ÷ 2⁶) = 2⁻² · 2¹ = 2⁻¹ = 1/2

d) (1⁸)⁹ = 1⁷² = 1

e) 125⁵ ÷ 5⁷ = (5³)⁵ ÷ 5⁷ = 5¹⁵ ÷ 5⁷ = 5¹⁵⁻⁷ = 5⁸

7. Aşağıdaki işlemlerin sonuçlarının en sade hâlini üslü ifade olarak yazınız.
Cevap:

a) (25⁴ · 8³) / 5⁻¹ = 10⁹

b) (9³ · (−25)⁴) / (27 · (−5)²) = 3³ · 5⁶

c) (2⁶ · 8⁻⁴) / (16⁴ · 128⁻²) = 2⁻⁸

ç) (81² · 3⁻⁵) / (3⁶ · (1/3²)⁴) = 3⁵

8.
2^a= 1/32 ve 3^-b = 1/27 olmak üzere 10^b·a üslü ifadesinin değeri kaç basamak doğal sayıdır?
Cevap:

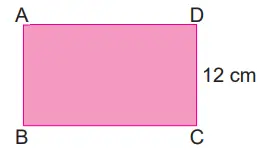
9. Uzun kenar uzunluğu 32 cm, kısa kenar uzunluğu 16 cm olan dikdörtgen şeklinde bir karton aşağıda verilmiştir. Bu karton birinci adımdaki gibi ortadan dikey kesilip yarısı, ardından ikinci adımdaki gibi ortadan yatay kesilip tekrar yarısı alınıyor. Sonra bu kesme işlemi 6. adım’a kadar devam ediyor.

Buna göre 6. adım sonunda elde edilen karton parçasının bir yüzünün alanı kaç santimetrekaredir?
Cevap:

Başlangıç: 32×16 cm

6. adım sonunda: 4×2 cm

Alan: 4 · 2 = 8 cm²

8. Sınıf Matematik Ders Kitabı Sayfa 44 Cevapları MEB Yayınları

Düşünme Zamanı

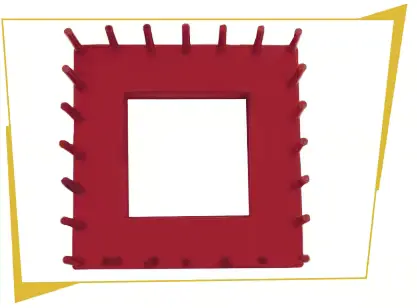
Aşağıda her birinde iki çubuk bulunan düzeneklere altlarındaki boncuklar eklenecektir.
Boncukların tamamını aynı renkler yan yana olacak şekilde ekleyerek üslü ifadeler oluşturunuz.
Boncuklar nasıl yerleştirilirse oluşacak üslü ifadelerin çarpımı olabilecek en büyük değere sahip olur? Bu üslü ifadeleri aşağıdaki noktalı yerlere yazınız.
Cevap:

a) Üst sol tarafa 2 kırmızı, alt sol tarafa 1 mavi eklenmeli.

b) Üst sol tarafa 2 mavi, alt sol tarafa 1 kırmızı eklenmeli.

c) Üst sol tarafa 1 kırmızı, üst sağ tarafa 2 mavi eklenmeli.

ç) Üst sol tarafa 1 mavi, alt sol tarafa 2 kırmızı eklenmeli.

a)
Eklemeler: 2 kırmızı → üst çubuğun sola (top_left), 1 mavi → alt çubuğun sola.
Oluşan ifadeler: (−5)⁴ ve 5⁻⁴
Sadeleştirilmiş: (−5)⁴ = 625, 5⁻⁴ = 1/625
Çarpım: 625 · 1/625 = 1

b)
Eklemeler: 1 kırmızı → alt çubuğun sola (bot_left), 2 mavi → üst çubuğun sola.
Oluşan ifadeler: 4³ ve (−4)⁻⁴
Sadeleştirilmiş: 4³ = 64, (−4)⁻⁴ = 1/256
Çarpım: 64 · 1/256 = 1/4

c)
Eklemeler: 1 kırmızı → üst çubuğun sola (top_left), 2 mavi → üst çubuğun sağa.
Oluşan ifadeler: (−5)⁷ ve (−4)¹
Sadeleştirilmiş: (−5)⁷ = −78125, (−4)¹ = −4
Çarpım: (−78125) · (−4) = 312500

Not: burada her iki ifade de negatif olduğu için çarpım pozitif ve büyük oluyor — bu yerleştirme en büyük sonucu veriyor.

ç)
Eklemeler: 2 kırmızı → alt çubuğun sola (bot_left), 1 mavi → üst çubuğun sola.
Oluşan ifadeler: 4⁻³ ve (−4)⁴
Sadeleştirilmiş: 4⁻³ = 1/64, (−4)⁴ = 256
Çarpım: 1/64 · 256 = 4

Sonraki Ödevler

• 8. Sınıf Matematik Ders Kitabı Sayfa 49-50-51. Cevapları MEB Yayınları
• 8. Sınıf Matematik Ders Kitabı Sayfa 52-53-54-55. Cevapları MEB Yayınları
• 8. Sınıf Matematik Ders Kitabı Sayfa 33-35-38-41. Cevapları MEB Yayınları
• 8. Sınıf Matematik Ders Kitabı Sayfa 29-30-31-32. Cevapları MEB Yayınları