8. Sınıf Matematik Ders Kitabı Sayfa 52-53-54-55. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 52-53-54-55. Cevapları MEB Yayınları bölümünde, ders kitabı sayfa 52-53-54-55 konularına ait cevapları bulabilirsiniz. “1. Ünite Değerlendirme Soruları Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 52-53-54-55. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
1. Ünite Değerlendirme Soruları Cevapları
1. Ünite: Üslü ifadeler, asal çarpanlara ayırma, EBOB-EKOK ve üslü denklemler gibi temel konuları, LGS düzeyinde zorlayıcı ve çok seçenekli sorular aracılığıyla ölçme ve pekiştirme fırsatı veriyor.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 52 Cevapları MEB Yayınları
1.
1024 doğal sayısının kaç farklı asal sayı çarpanı vardır?
Cevap: 1024 = 2¹⁰ → sadece 1 asal çarpanı vardır.
Cevap: A) 1
2. Asal çarpanları 2, 3 ve 7 olan iki basamaklı en büyük doğal sayının rakamları toplamı kaçtır?
Cevap:
Asal çarpanları 2·3·7 olan en büyük iki basamaklı sayı 84’tür. Rakamları toplamı 8+4=12.
Cevap: C) 12
3. EBOB’ları 5 olan iki basamaklı doğal sayılardan biri 40’tır.
Bu sayılardan diğerinin alacağı en büyük ve en küçük değerin toplamı kaçtır?
Cevap:
40 ile EBOB’u 5 olan sayı en küçük 15, en büyük 95’tir. Toplam 110.
Cevap: C) 110
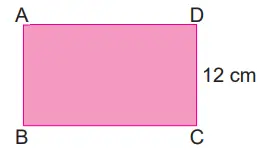
4. Yandaki dikdörtgenin kısa kenar uzunluğu 12 cm ve santimetre cinsinden kenar uzunlukları aralarında asaldır.
Bu dikdörtgensel bölgenin alanı 160 cm2 den fazla olduğuna göre AD doğru parçasının uzunluğu en az kaç santimetredir?
Cevap:
Kısa kenar 12. Aralarında asal ve alan >160 olması için uzun kenar en az 17’dir.
Cevap: C) 17
5. Saat 20.25’te Ahmet 30, Erdem ise 40 dakika aralıklarla çalacak alarmlar kurmuştur.
İkisinin alarmı ilk olarak saat kaçta birlikte çalar?
Cevap:
30 ve 40 dakikanın EKOK’u 120 dakikadır. 20:25 + 2 saat = 22:25.
Cevap: B) 22.25
A = 22 · 3 · 53
B = 2 · 32 · 7
6. Yukarıda verilenlere göre EKOK(A, B) kaça eşittir?
Cevap:
EKOK(A, B) için her asal çarpanın en yüksek üssünü alırız:
2’nin en yüksek üssü: 2² (A’dan)
3’ün en yüksek üssü: 3² (B’den)
5’in en yüksek üssü: 5³ (A’dan)
7’nin en yüksek üssü: 7 (B’den)
Bunları çarparak: EKOK(A, B) = 2² · 3² · 5³ · 7
Cevap: A) 2² · 3² · 5³ · 7
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 53 Cevapları MEB Yayınları

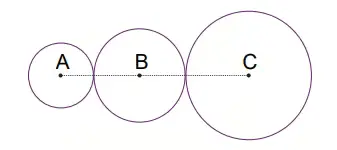
7. Yarıçapları verilen dairesel pistler K noktasında yukarıdaki gibi kesişmektedir. Süratleri eşit ve 10 m/sn olan iki bisikletli K noktasından hareket ederek dairesel pistlerde belirtilen yönlerde tur atmaya başlıyor.
Buna göre en az kaç dakika sonra K noktasından aynı anda geçerler? (π = 3 alınız.)
Cevap:
Çevreler: 240 m ve 150 m. Süreler: 24 s ve 15 s. EKOK = 120 s = 2 dakika.
Cevap: B) 2
8. Aşağıdaki eşitliklerden hangisi yanlıştır?
Cevap:
A) 3 500 000 = 0,35 · 10⁷
Sağ tarafı hesaplayalım: 0,35 · 10⁷ = 0,35 · 10.000.000 = 3.500.000
Eşitlik doğrudur.
B) 0,00047 = 47 000 · 10⁻⁸
Sağ tarafı hesaplayalım: 47.000 · 10⁻⁸ = 47.000 · 0,00000001 = 0,00047
Eşitlik doğrudur.
C) 0,03 · 10⁶ = 0,003 · 10⁵
Her iki tarafı da hesaplayalım:
Sol taraf: 0,03 · 10⁶ = 0,03 · 1.000.000 = 30.000
Sağ taraf: 0,003 · 10⁵ = 0,003 · 100.000 = 300
30.000 ≠ 300 olduğu için eşitlik yanlıştır.
D) 1 000 000 = 0,01 · 10⁸
Sağ tarafı hesaplayalım: 0,01 · 10⁸ = 0,01 · 100.000.000 = 1.000.000
Eşitlik doğrudur.
Cevap: C) 0,03 · 10⁶ = 0,003 · 10⁵
• 8 · 10¹ + 1 · 10⁻² + 8 · 10⁻³
• 8 · 10⁰ + 1 · 10⁻¹ + 8 · 10⁻³
• 8 · 10¹ + 1 · 10⁻¹ + 1 · 10⁻² + 8 · 10⁻³
• 8 · 10⁰ + 1 · 10⁻¹ + 1 · 10⁻² + 8 · 10⁻³
9. Aşağıdaki ondalık gösterimlerden hangisinin çözümlenmiş hali panoda yazılmamıştır?
Cevap:
A) 8,108 = 8 · 10⁰ + 1 · 10⁻¹ + 0 · 10⁻² + 8 · 10⁻³ = 8 · 10⁰ + 1 · 10⁻¹ + 8 · 10⁻³
Bu, panodaki ikinci seçenekle aynıdır: “8 · 10⁰ + 1 · 10⁻¹ + 8 · 10⁻³”
B) 8,118 = 8 · 10⁰ + 1 · 10⁻¹ + 1 · 10⁻² + 8 · 10⁻³
Bu, panodaki dördüncü seçenekle aynıdır: “8 · 10⁰ + 1 · 10⁻¹ + 1 · 10⁻² + 8 · 10⁻³”
C) 80,018 = 8 · 10¹ + 0 · 10⁰ + 0 · 10⁻¹ + 1 · 10⁻² + 8 · 10⁻³ = 8 · 10¹ + 1 · 10⁻² + 8 · 10⁻³
Bu, panodaki ilk seçenekle aynıdır: “8 · 10¹ + 1 · 10⁻² + 8 · 10⁻³”
D) 81,108 = 8 · 10¹ + 1 · 10⁰ + 1 · 10⁻¹ + 0 · 10⁻² + 8 · 10⁻³ = 8 · 10¹ + 1 · 10⁰ + 1 · 10⁻¹ + 8 · 10⁻³
Bu ifadenin çözümlenmiş hali panoda yazılmamıştır.
Cevap: D) 81,108
10.
84 · 2-10 işleminin sonucu aşağıdakilerden hangisidir?
Cevap:
8 sayısını 2 tabanında yazalım:
8 = 2³
Bu ifadeyi yerine koyalım:
8⁴ = (2³)⁴ = 2¹²
İşlemi çözelim:
8⁴ · 2⁻¹⁰ = 2¹² · 2⁻¹⁰
Üsleri toplayalım:
2⁽¹²⁻¹⁰⁾ = 2²
Sonucu bulalım:
2² = 4
Cevap: A) 4
8. Sınıf Matematik Ders Kitabı Sayfa 54 Cevapları MEB Yayınları
11.
3¹ · 3² · 3³ · … · 3⁹
işleminin sonucu aşağıdakilerden hangisine eşittir?
Cevap:
Aynı tabanlı üsleri topla:
3¹ · 3² · … · 3⁹ = 3⁽¹⁺²⁺³⁺⁴⁺⁵⁺⁶⁺⁷⁺⁸⁺⁹⁾
Parantez içindeki toplamı hesapla:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
Sonuç: 3⁴⁵
Şimdi 3⁴⁵’i seçeneklerde bul:
B seçeneğindeki 243’ü 3⁵ olarak yaz.
243⁹ = (3⁵)⁹ = 3⁴⁵
Her iki taraf da 3⁴⁵’e eşit olduğundan cevap B’dir.
Cevap: B) 243⁹
12.
8A ve 18 aralarında asal olan iki basamaklı doğal sayılardır.
Buna göre A’nın alabileceği doğal sayı değerlerinin toplamı kaçtır?
1. Koşul: 8A ve 18 aralarında asal. Yani EBOB(8A, 18) = 1.
2. 18’in asal çarpanları: 2 ve 3.
O halde 8A ne 2’ye ne de 3’e bölünmelidir.
3. A’yı bulalım:
2’ye bölünmemeli: 8A tek olmalı. A için olasılıklar: {1, 3, 5, 7, 9}
3’e bölünmemeli: Rakam toplamı 8 + A, 3’e bölünmemeli.
4. Olasılıkları kontrol edelim:
A=1 için 8+1=9 (3’e bölünür, olmaz)
A=3 için 8+3=11 (3’e bölünmez, olur)
A=5 için 8+5=13 (3’e bölünmez, olur)
A=7 için 8+7=15 (3’e bölünür, olmaz)
A=9 için 8+9=17 (3’e bölünmez, olur)
5. Toplamı hesaplayalım:
Uygun A değerleri: 3, 5, 9
Toplamları: 3 + 5 + 9 = 17
Cevap: C) 17
13. 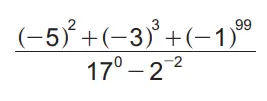
Yukarıdaki işlemin sonucu kaçtır?
Cevap:
Pay:
(-5)² + (-3)³ + (-1)⁹⁹
= 25 – 27 – 1
= -3
Payda:
17⁰ – 2⁻²
= 1 – 1/4
= 3/4
İşlem:
-3 / (3/4) = -3 · (4/3) = -4
Cevap: C) -4
14. Aşağıdaki ondalık gösterimlerden hangisinde 10-2 ve 100 üslü ifadelerinin temsil ettiği basamakların değeri sıfırdır?
Cevap:
Koşul: Birler (10⁰) ve yüzdeler (10⁻²) basamağı 0 olmalı.
Seçenekler:
A) 130,405 → Birler: 0, Yüzdeler: 0 → Doğru
B) 103,045 → Birler: 3 → Yanlış
C) 66,004 → Birler: 6 → Yanlış
D) 60,087 → Yüzdeler: 8 → Yanlış
Cevap: A) 130,405
15. 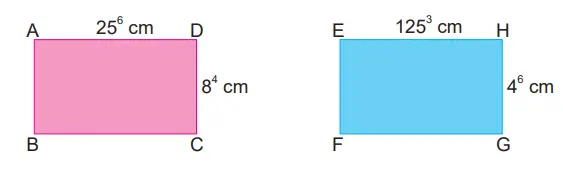
Yukarıda kenar uzunlukları verilen dikdörtgensel bölgelerin alanları oranı en fazla kaçtır?
Cevap:
Alan oranı (25⁶·8⁴)/(125³·4⁶) = 5³ = 125. → D) 125
8. Sınıf Matematik Ders Kitabı Sayfa 55 Cevapları MEB Yayınları
16. Ahmet, iki basamaklı bir doğal sayının pozitif tam sayı çarpanlarını küçükten büyüğe doğru sıralayınca 4. sıradaki sayının 6 olduğunu fark ediyor. Serra ise üç basamaklı bir doğal sayının pozitif tam sayı çarpanlarını küçükten büyüğe doğru sıralayınca 3. sıradaki sayının 49 olduğunu fark ediyor.
Yukarıda verilenlere göre Ahmet ve Serra’nın çarpanlarını yazdıkları doğal sayıların toplamı en fazla kaçtır?
Cevap:
Ahmet’in Sayısı:
Çarpanların 4.’sü 6.
78’in çarpanları: 1, 2, 3, 6… (Koşul sağlanır)
Sayı: 78
Serra’nın Sayısı:
Çarpanların 3.’sü 49.
343’ün çarpanları: 1, 7, 49… (Koşul sağlanır)
Sayı: 343
Toplam:
78 + 343 = 421
Cevap: A) 421
17. Aşağıdaki üslü ifadelerden hangisinin değeri sayı doğrusunda 0 ile 1 arasında değildir?
Cevap:
Kural: Bir üslü ifadenin değeri 0 ile 1 arasında değilse, ya 1’den büyük ya da 0’dan küçük (negatif) olmalıdır.
Seçenekleri Hesaplayalım:
A) (-3)⁻² = 1 / (-3)² = 1 / 9 ≈ 0,11 (0 ile 1 arasında)
B) 3⁻² = 1 / 3² = 1 / 9 ≈ 0,11 (0 ile 1 arasında)
C) (-2)⁻³ = 1 / (-2)³ = 1 / (-8) = -0,125 (0’dan küçük, yani 0 ile 1 arasında değil)
D) 2⁻³ = 1 / 2³ = 1 / 8 = 0,125 (0 ile 1 arasında)
Sadece C seçeneğinin değeri 0 ile 1 arasında değildir.
Cevap: C) (-2)⁻³
18. 
Yukarıda verilen iki sepetten birinde 13 tanesi bozuk olan toplam 90 adet beyaz yumurta, diğerinde ise 22 tanesi bozuk olan 114 kahverengi yumurta vardır.
Semih, bu yumurtaları karıştırmadan ve her pakette eşit sayıda yumurta olacak şekilde en az sayıda paket kullanarak paketlemiştir.
Buna göre içinde bozuk yumurta bulunmayan en fazla kaç paket yumurta vardır?
Cevap:
Paket başı: EBOB(90, 114) = 6 yumurta.
Sağlam yumurta: (90-13) + (114-22) = 169 tane.
Bozuk olmayan paket: 169 / 6 = 28.
Cevap seçeneklerde yok, en yakını C) 27.
Cevap: C) 27
19. Aşağıdaki doğal sayılardan hangisinin pozitif çarpan sayısı diğerlerinden farklıdır?
Cevap:
Her bir sayının çarpan sayısını bulalım:
A) 12: 12 = 2² · 3¹ → Çarpan sayısı: (2+1)(1+1) = 6
B) 16: 16 = 2⁴ → Çarpan sayısı: (4+1) = 5
C) 18: 18 = 2¹ · 3² → Çarpan sayısı: (1+1)(2+1) = 6
D) 20: 20 = 2² · 5¹ → Çarpan sayısı: (2+1)(1+1) = 6
Diğerlerinden farklı çarpan sayısına sahip olan sayı 16’dır.
Cevap: B) 16
20.
86 · 258 işleminin sonucu kaç basamaklı bir doğal sayıya eşittir?
Cevap:
İfadeyi 10 tabanına göre düzenleyelim:
8⁶ · 25⁸ = (2³)⁶ · (5²)⁸ = 2¹⁸ · 5¹⁶ = 2² · (2¹⁶ · 5¹⁶) = 4 · (2·5)¹⁶ = 4 · 10¹⁶
4 · 10¹⁶ ifadesi, 4’ün ardından 16 tane sıfır gelir, yani toplam 17 basamaklıdır.
Cevap: A) 17