8. Sınıf Matematik Ders Kitabı Sayfa 58-60-61-62-63. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 58-60-61-62-63. Cevapları MEB Yayınları bölümünde, ders kitabı sayfa 58-59-60-61-62-63 konularına ait cevapları bulabilirsiniz. “Tam Kare Pozitif Tam Sayılar ve Karekökleri Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 58-60-61-62-63. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Tam Kare Pozitif Tam Sayılar ve Karekökleri Cevapları
2. Ünite 1. Bölüm Kareköklü İfadeler: Kare motif aparatında düğüm sayısı, kenar sayısına bağlı olarak kare sayılar (1, 4, 9, 16 gibi) olabilir. Tam kare sayılar ve karekökleri, matematikte düzenli örüntüler oluşturarak geometrik şekillerin alanlarını ve kenar uzunluklarını hesaplamamıza yardımcı olur.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 58 Cevapları MEB Yayınları
Kare motif aparatı, karesel bir zeminin kenarlarına eşit aralıklarla dikilmiş plastik çubuklardan oluşur. Karşılıklı plastik çubuklara ipler gerilir ve bu iplerin kesişimlerine düğümler atılır. Atılan düğümlerle çeşitli kare motifler dokunur.
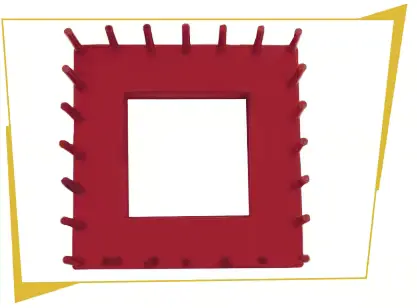
Sizce bir kare motifteki düğüm sayısı hangi doğal sayılar olabilir?
Cevap: Soruda bahsedilen kare motif aparatı, kenarlarında eşit aralıklarla çubuklar bulunan bir kare çerçevedir. Bu çubuklar arasına ipler gerildiğinde, iplerin kesiştiği noktalar (yani karelerin içindeki düğümler) bir kare ağ oluşturur.
Eğer her kenarda 𝑛 tane çubuk varsa:
Karşılıklı çubuklar arasında 𝑛 − 1 tane ip gerilir.
Bu iplerin kesiştiği düğüm sayısı ise (n – 1) × (n – 1) olur.
Sonuç olarak: Bir kare motifteki düğüm sayısı 1, 4, 9, 16, 25, 36 ve 49, … gibi kare sayılar olabilir.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 60 Cevapları MEB Yayınları
Sıra Sizde 1
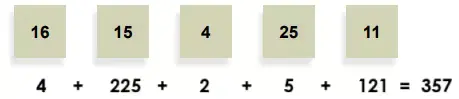
Yukarıdaki kartların her birinin bir yüzünde tam kare doğal sayı, diğer yüzünde ise bu tam kare doğal sayının karekökü yazmaktadır.
Buna göre bu kartların görünmeyen yüzlerindeki doğal sayıların toplamı en az kaç olur?
Cevap:
Her kartın iki yüzü (k², k) şeklinde bir çifttir. Görünen sayıya göre hangi yüz olduğu belli olur:
16 görünüyorsa, ya 16 = k² → k = 4 olur, ya da 16 = k → k² = 256 olur. En az değer 4’tür.
15 görünüyorsa bu bir tam kare olmadığından 15 = k olur; gizli yüz 15² = 225.
4 görünüyorsa, ya 4 = k² → k = 2, ya da 4 = k → k² = 16. En az değer 2’dir.
25 görünüyorsa, ya 25 = k² → k = 5, ya da 25 = k → k² = 625. En az değer 5’tir.
11 görünüyorsa 11 tam kare olmadığından 11 = k olur; gizli yüz 11² = 121.
Gizli sayıların en küçük toplamı:
4 + 225 + 2 + 5 + 121 = 357
8. Sınıf Matematik Ders Kitabı Sayfa 61 Cevapları MEB Yayınları
Alıştırmalar Cevapları
1. 100, 144, 289 ve 324 sayılarının kareköklerini bulunuz.
Cevap:
√100, √144, √289, √324 işlemleri
√100 = 10 çünkü 10·10 = 100.
√144 = 12 çünkü 12·12 = 144.
√289 = 17 çünkü 17·17 = 289.
√324 = 18 çünkü 18·18 = 324.
2. Kare şeklindeki bir duvar kaplama materyalinin görünen yüzünün alanı 900 cm2 olduğuna göre bir kenarının uzunluğu kaç santimetredir?
Cevap: 30 cm.
Kenar uzunluğu (alan = 900 cm²)
Kare alanı = kenar².
Kenar = √900.
√900 = 30 çünkü 30·30 = 900.
3. √2² – √25 + √3⁴ işleminin sonucu kaçtır?
Cevap: 6
√(2²) − √25 + √(3⁴) işlemi
√(2²) = √4 = 2
√25 = 5
√(3⁴) = √81 = 9 (çünkü 3⁴ = 81)
İşlem:
2 − 5 + 9 = (2 − 5) + 9 = −3 + 9 = 6
Yukarıda verilen tam sayı örüntüsünün terimlerinden tam kare olanların toplamı kaçtır?
Cevap: 52
Örüntü: 96, 86, 76, 66, … (her adım −10) — tam kare olanların toplamı
Terimleri yazalım: 96, 86, 76, 66, 56, 46, 36, 26, 16, 6, …
Hangileri tam karedir? 36 = 6² ve 16 = 4². Diğerleri tam kare değil.
Toplam = 36 + 16 = 52.
5. Basamaklarındaki rakamların toplamı 9 olan, iki basamaklı tam kare doğal sayıların toplamı kaçtır?
Cevap: 117
İki basamaklı tam kare doğal sayılar ve basamaklar toplamı 9 olanların toplamı
İki basamaklı tam kareler: 16 (1+6=7), 25 (2+5=7), 36 (3+6=9), 49 (4+9=13), 64 (6+4=10), 81 (8+1=9).
Basamakları toplamı 9 olanlar: 36 ve 81.
Toplam = 36 + 81 = 117.
6 Aşağıdaki ifadelerden doğru olanların başına “D”, yanlış olanların başına “Y” yazınız.
Cevap:
“−5’in karesi 3’ün karesinden büyüktür.”
(−5)² = 25, 3² = 9 → 25 > 9 → D.
b) “Karesi 49 olan 7’den başka tam sayı yoktur.”
7² = 49 ve (−7)² = 49 → 49’un karesi olan sayılar 7 ve −7’dir → ifade yanlış → Y.
c) “Üç basamaklı en küçük tam kare pozitif tam sayı 121’dir.”
En küçük üç basamaklı sayı 100’dür; 100 = 10² olduğundan en küçük üç basamaklı tam kare 100’dür → ifade yanlış → Y.
d) “2³ + 2³ ifadesi tam kare sayıdır.”
2³ + 2³ = 8 + 8 = 16 ve 16 = 4² → tam karedir → D.
e) “√16 ifadesi 2’nin karesine eşittir.”
√16 = 4 ve 2’nin karesi 2² = 4 → eşittir → D.

8. Sınıf Matematik Ders Kitabı Sayfa 62 Cevapları MEB Yayınları
7) Aynı yıl doğan Seher ve Bahar’ın doğum tarihlerindeki gün ve ayı gösteren sayılar, ayrı ayrı tam kare doğal sayılardır.
Buna göre Seher ile Bahar arasındaki yaş farkı en fazla kaç ay ve gündür?
Cevap:
Aynı yıl doğan Seher ve Bahar’ın gün ve ay sayıları ayrı ayrı tam kare doğal sayılardır.
Ay için tam kareler: 1 (Ocak), 4 (Nisan), 9 (Eylül).
Gün için tam kareler: 1, 4, 9, 16, 25.
En erken tarih: 1 Ocak (gün=1, ay=1).
En geç tarih: 25 Eylül (gün=25, ay=9).
1 Ocak → 1 Eylül arası = 8 ay (Ocak→Eylül = 8 tam ay).
1 Eylül → 25 Eylül = 24 gün.
Sonuç: 8 ay 24 gün.
8) Yandaki yamuğun alanı santimetrekare cinsinden tam kare doğal sayıya eşittir.
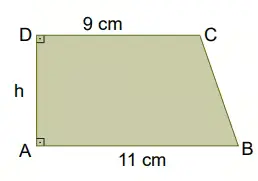
Buna göre yamuğun yüksekliği tam sayı olarak en az kaç santimetredir?
Cevap: 10 cm
Yamuğun üst tabanı = 9 cm
Alt tabanı = 11 cm
Yükseklik = h
Yamuğun alanı:
A = ((9 + 11) / 2) × h
A = (20 / 2) × h
A = 10h
Alan santimetrekare cinsinden tam kare doğal sayı olmalıdır.
Yani 10h = k² olmalıdır.
k² ifadesi 10’a tam bölünebilmesi için k’nin en az 10’un katı olması gerekir.
k = 10 → k² = 100 olur.
10h = 100
h = 10
9) Bir kapta 4 litre sıvı sabun vardır. Bu sıvı sabun, her biri mililitre cinsinden tam kare doğal sayı olan eşit hacimli sabunluklara tam olarak doldurulacaktır.
Bu iş sonunda kapta sıvı sabun kalmayacağına göre en az kaç tane sıvı sabunluk tam olarak doldurulabilir?
Cevap: 10 sabunluk
Toplam sıvı sabun miktarı = 4 litre = 4000 mL
Her bir sabunluk hacmi mililitre cinsinden tam kare doğal sayı olacak.
Ayrıca kapta sabun kalmamalı → 4000, o tam kare sayıya tam bölünmeli.
4000’in asal çarpanlarına ayrılması:
4000 = 2⁵ × 5³
Bir sayının tam kare olması için üsleri çift olmalıdır.
En büyük tam kare bölen için üsleri aşağıya yuvarlayalım:
2⁴ × 5² = 16 × 25 = 400
Yani en büyük tam kare bölen 400 mL’dir.
4000 ÷ 400 = 10
10)
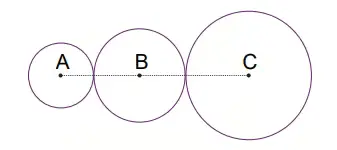
Yukarıda kenarları çakışık üç karesel bölge ve bunların alan ölçüleri verilmiştir.
Bu karelerin her birinin alanı üç basamaklı tam kare doğal sayı olduğuna göre yukarıdaki şeklin çevresi en az kaç santimetredir?
Cevap: 102 cm
Verilen üç basamaklı tam kareler: 196, 169, 100
Bunların kenar uzunlukları:
196 → 14 cm
169 → 13 cm
100 → 10 cm
Yatay açık kenarlar (üst + alt) = 2 * (14 + 13 + 10) = 2 * 37 = 74
Dikey açık kenarlar:
– Sol dış dikey = 14
– Sağ dış dikey = 10
– Ortadaki yükseklik farkları = (14 – 13) + (13 – 10) = 1 + 3 = 4
Toplam dikey = 14 + 10 + 4 = 28
Toplam çevre = yatay açık kenarlar + dikey açık kenarlar
= 74 + 28
= 102 cm
8. Sınıf Matematik Ders Kitabı Sayfa 63 Cevapları MEB Yayınları
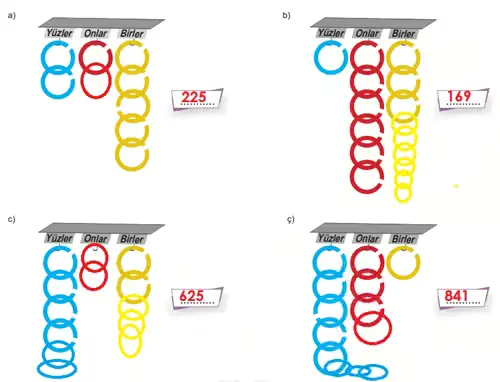
Aşağıda fiyatları altlarında yazan üç farklı renkte halka verilmiştir.
Bu halkalardan mavi renkli olanlar düzenekte yüzler basamağına, kırmızı renkli olanlar onlar basamağına ve sarı renkli olanlar ise birler basamağına asılarak üç basamaklı sayılar örnekteki gibi modellenecektir.
Aşağıdaki modellere en az maliyetle yeni halkalar ekleyerek üç basamaklı tam kare sayılar oluşturunuz. Oluşturduğunuz sayıları modellerin yanına yazınız.
Cevap:
a) Başlangıç: 215
Mevcut: 2 | 1 | 5 → 215
Bazı üç basamaklı tam kareler ve gereken ek halkalar (hedef_basamak − mevcut_basamak, sadece ≥0 olanlar geçerli):
225 (15²) = (2,2,5): +0, +1, +0 → 1 halka
256 (16²) = (2,5,6): +0, +4, +1 → 5 halka
289 (17²) = (2,8,9): +0, +7, +4 → 11 halka
daha büyükleri daha çok ek gerektirir.
En az ekleme: 225 (15²) → +1 onlar.
Sonuç: 215 → 225 (ek: 0 mavi, +1 kırmızı, 0 sarı)
b) Başlangıç: 163
Mevcut: 1 | 6 | 3 → 163
Uygun tam kareler (her basamak hedef ≥ mevcut):
169 (13²) = (1,6,9): +0, +0, +6 → 6 halka
196 (14²) = (1,9,6): +0, +3, +3 → 6 halka
256 (16²) = (2,5,6): tens 5 < 6 → geçersiz (azaltma yok)
Diğer geçerli kareler genelde daha fazla ek ister.
En az ekleme: 169 (13²) veya 196 (14²) — eşit, ama küçük olanı alalım: 169.
Sonuç: 163 → 169 (ek: 0 mavi, 0 kırmızı, +6 sarı)
c) Başlangıç: 402
Mevcut: 4 | 0 | 2 → 402
Uygun tam kareler (hedef basamak ≥ mevcut basamak):
441 (21²) = (4,4,1): birler 1 < 2 → geçersiz
484 (22²) = (4,8,4): +0, +8, +2 → 10 halka
529 (23²) = (5,2,9): +1, +2, +7 → 10 halka
576 (24²) = (5,7,6): +1, +7, +4 → 12 halka
625 (25²) = (6,2,5): +2, +2, +3 → 7 halka ← en az
Diğerleri daha fazla ek ister.
En az ekleme: 625 (25²) → +2 mavi, +2 kırmızı, +3 sarı (toplam 7 halka).
Sonuç: 402 → 625 (ek: +2 yüz, +2 onlar, +3 birler)
ç) Başlangıç: 531
Mevcut: 5 | 3 | 1 → 531
Uygun tam kareler:
576 (24²) = (5,7,6): +0, +4, +5 → 9 halka
625 (25²) = (6,2,5): tens 2 < 3 → geçersiz
676 (26²) = (6,7,6): +1, +4, +5 → 10 halka
784 (28²) = (7,8,4): +2, +5, +3 → 10 halka
841 (29²) = (8,4,1): +3, +1, +0 → 4 halka ← en az
961 (31²) = (9,6,1): +4, +3, +0 → 7 halka
En az ekleme: 841 (29²) → +3 mavi, +1 kırmızı, +0 sarı (toplam 4 halka).
Sonuç: 531 → 841 (ek: +3 yüz, +1 onlar, +0 birler)