8. Sınıf Matematik Ders Kitabı Sayfa 66-67-68-69. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 66-67-68-69. Cevapları MEB Yayınları bölümünde, ders kitabı sayfa 64-65-66-67-68-69 konularına ait cevapları bulabilirsiniz. “Tam Kare Olmayan Kareköklü İfadenin Hangi İki Doğal Sayı Arasında Olduğunu Belirleme Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 66-67-68-69. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Tam Kare Olmayan Kareköklü İfadenin Hangi İki Doğal Sayı Arasında Olduğunu Belirleme
2. Ünite 1. Bölüm Kareköklü İfadeler: Tam kare olmayan sayıların karekökleri, iki ardışık tam sayı arasında yer alır ve genellikle bu sayılardan birine daha yakındır. Kareköklerin değerini tahmin etmek için komşu tam kareleri kullanarak karşılaştırma yapabiliriz.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 66 Cevapları MEB Yayınları
Sıra Sizde 1
√43 ve √90 ifadelerinin hangi doğal sayılar arasında ve bu sayılardan hangisine daha yakın olduğunu ayrı ayrı bulunuz.
Cevap:
√43 ifadesi için:
6² = 36 ve 7² = 49 olduğundan, 36 < 43 < 49, yani √43, 6 ve 7 doğal sayıları arasındadır.
43 – 36 = 7 ve 49 – 43 = 6 olduğundan, 43 sayısı 49’a (7’nin karesine) daha yakındır.
√43 ifadesi 6 ve 7 doğal sayıları arasında ve 7’ye daha yakındır.
√90 ifadesi için:
9² = 81 ve 10² = 100 olduğundan, 81 < 90 < 100, yani √90, 9 ve 10 doğal sayıları arasındadır.
90 – 81 = 9 ve 100 – 90 = 10 olduğundan, 90 sayısı 81’e (9’un karesine) daha yakındır.
√90 ifadesi 9 ve 10 doğal sayıları arasında ve 9’a daha yakındır.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 67 Cevapları MEB Yayınları
Düşünme Zamanı
Aşağıda verilen soruları yönergeye göre cevaplayınız.
Üzerlerinde rakamları birbirinden farklı olan doğal sayıların yazılı olduğu kartlar;
kartın üzerindeki sayı bir tam kare sayı ise kareköküne eşit numaralı kutuya, kartın üzerindeki sayı tam kare olmayan doğal sayı ise kareköküne en yakın numaralı kutuya atılacaktır.
Son durumda her kutuda bir kart olacaktır.
a) Kartlar üzerinde verilen sayılar iki basamaklı olduğuna göre A, B, C, D ve E harflerinin alacağı değerler toplamı en az kaçtır?
Cevap: 7
Amaç: A+B+C+D+E toplamını en az yapmak.
Sabitler:
6D → 8. kutu
8E → 9. kutu
Kalanlar (5, 6, 7. kutular için):
3C=30 → 5. kutu (C=0)
B2=32 → 6. kutu (B=3)
A3=43 → 7. kutu (A=4)
Toplam: 4 + 3 + 0 + 0 + 0 = 7
b) Kartlar üzerinde verilen sayılar üç basamaklı olduğuna göre K, L, M, N ve P harflerinin alacağı değerler toplamı en çok kaçtır?
Cevap: 15
Amaç: K+L+M+N+P toplamını en çok yapmak.
Sabitler:
M56=156 → 12. kutu (M=1)
1P2=102 → 10. kutu (P=0)
Kalanlar (11, 13, 14. kutular için):
1K0=130 → 11. kutu (K=3)
18L=182 → 13. kutu (L=2)
18N=189 → 14. kutu (N=9)
Toplam: 3 + 2 + 1 + 9 + 0 = 15
8. Sınıf Matematik Ders Kitabı Sayfa 68 Cevapları MEB Yayınları
Alıştırmalar
1) Aşağıdaki kareköklü ifadelerin hangi ardışık doğal sayılar arasında olduğunu belirleyiniz.
Cevap:
a) √18: √16 = 4 ve √25 = 5 olduğundan, √18 sayısı 4 ile 5 arasındadır.
b) √43: √36 = 6 ve √49 = 7 olduğundan, √43 sayısı 6 ile 7 arasındadır.
c) √58: √49 = 7 ve √64 = 8 olduğundan, √58 sayısı 7 ile 8 arasındadır.
ç) √85: √81 = 9 ve √100 = 10 olduğundan, √85 sayısı 9 ile 10 arasındadır.
2) Aşağıdaki kareköklü ifadelerin en yakın olduğu doğal sayıyı belirleyiniz.
Cevap:
Bu soruda, kareköklü ifadelerin değerine en yakın tam sayıyı bulmamız istenmektedir. Bunun için karekökün kendisine en yakın tam sayıyı buluruz.
a) √21: √16 = 4 ve √25 = 5’tir. √21 sayısı, 21-16=5 ve 25-21=4 olduğundan 5’e daha yakındır. En yakın doğal sayı 5‘tir.
b) √30: √25 = 5 ve √36 = 6’dır. √30 sayısı, 30-25=5 ve 36-30=6 olduğundan 5’e daha yakındır. En yakın doğal sayı 5‘tir.
c) √42: √36 = 6 ve √49 = 7’dir. √42 sayısı, 42-36=6 ve 49-42=7 olduğundan 6’ya daha yakındır. En yakın doğal sayı 6‘dır.
ç) √92: √81 = 9 ve √100 = 10’dur. √92 sayısı, 92-81=11 ve 100-92=8 olduğundan 10’a daha yakındır. En yakın doğal sayı 10‘dur.
3) Bir doğal sayının karekökü 7 ile 8 doğal sayıları arasındadır.
Buna göre bu doğal sayının alabileceği en büyük değer kaçtır?
Cevap: 63
Bir sayının karekökü 7 ile 8 arasında ise, sayı kendisi 7² ve 8² arasında olmalıdır.
- 7² = 49
- 8² = 64
Dolayısıyla sayı 49 ile 64 arasındadır. Bu aralıktaki en büyük doğal sayı, 64’ten bir eksik olan sayıdır.
- 64 – 1 = 63
4) 13 ve 91 doğal sayılarının karekökleri arasındaki doğal sayıların toplamını bulunuz.
Cevap: 39
Öncelikle 13 ve 91 sayılarının kareköklerini bulalım.
√13 ≈ 3.60
√91 ≈ 9.53
Şimdi, 3.60 ile 9.53 arasındaki doğal sayıları bulalım. Bu aralık, 4’ten başlayıp 9’a kadar devam eder.
Aralıktaki doğal sayılar: 4, 5, 6, 7, 8, 9
Bu sayıların toplamını hesaplayalım:
Toplam = 4 + 5 + 6 + 7 + 8 + 9 = 39
5) Sayı doğrularında verilen kareköklü ifadelere sağdan ve soldan en yakın olan doğal sayıları belirleyiniz.
Cevap:
Bu soruda, verilen kareköklü ifadelerin değerinden küçük ve büyük olan en yakın tam sayıları (yani taban ve tavan sayılarını) bulmamız istenmektedir.
a) √55:
√49 = 7 ve √64 = 8 olduğundan, √55 sayısı 7 ile 8 arasındadır.
Soldan en yakın doğal sayı (taban): 7
Sağdan en yakın doğal sayı (tavan): 8
b) √132:
√121 = 11 ve √144 = 12 olduğundan, √132 sayısı 11 ile 12 arasındadır.
Soldan en yakın doğal sayı (taban): 11
Sağdan en yakın doğal sayı (tavan): 12
c) √265:
√256 = 16 ve √289 = 17 olduğundan, √265 sayısı 16 ile 17 arasındadır.
Soldan en yakın doğal sayı (taban): 16
Sağdan en yakın doğal sayı (tavan): 17
ç) √310:
√289 = 17 ve √324 = 18 olduğundan, √310 sayısı 17 ile 18 arasındadır.
Soldan en yakın doğal sayı (taban): 17
Sağdan en yakın doğal sayı (tavan): 18
8. Sınıf Matematik Ders Kitabı Sayfa 69 Cevapları MEB Yayınları
6) Tuba Hanım, elindeki 35 metrelik ipin √250 metresini kullanmıştır.
Geriye kalan ipin uzunluğunun metre cinsinden değerinin hangi doğal sayıya daha yakın olduğunu bulunuz.
Cevap: 19
Tuba Hanım elindeki 35 m ipin (√250) metresini kullanmıştır.
(√250 = 5√10 ≈ 5 · 3.1623 = 15.811) (yaklaşık).
Kalan ip = 35 – √250 ≈ 35 – 15.811 = 19.189.
Bu değer 19’a daha yakındır.
7) Akif’in mekanik kaleminin ucunun boyu √91 santimetredir.
Bir saatte ortalama 1,5 santimetre uç kullanan Akif’in 3 saat sonra kaleminde kalan ucun boyunun santimetre cinsinden hangi doğal sayıya daha yakın olduğunu bulunuz.
Cevap: 5
Akif’in uç uzunluğu √91 cm.
(√91) için (9² = 81, 10² = 100) olduğundan √91 ≈ 9.539.
3 saatte tüketilen uç = 3 · 1.5 = 4.5 cm.
Kalan = √91 – 4.5 ≈ 9.539 – 4.5 = 5.039.
Bu değer 5’e daha yakındır.
8) Zehra’nın silgisinin boyu 5 ile 6 santimetre arasında olup 6 santimetreye daha yakındır.
Buna göre Zehra’nın silgisinin boyunun santimetre cinsinden hangi doğal sayıların karekökü olarak ifade edilebileceğini bulunuz.
Silgi boyu 5 ile 6 arasında ve 6’ya daha yakın ⇒ silgi boyu >5.5 ve <6.
Yani √n ∈ (5.5, 6). Kare alırsak:
(5.5)² = 30.25, 6² = 36.
Doğal n için 30.25 < n < 36 ⇒ n = 31, 32, 33, 34, 35.
Cevap: √31, √32, √33, √34, √35 (yani 31–35 sayıları).
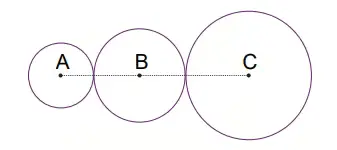
9) Dairenin alanı = π · r² formülü ile bulunur
Yukarıda verilen merkezleri aynı doğru üzerinde olan üç dairenin alanı küçükten büyüğe doğru sırasıyla 75 cm² , 108 cm² ve 144 cm² dir.
Buna göre A noktası ile C noktası arasındaki mesafenin cm cinsinden hangi doğal sayıya daha yakın olduğunu bulunuz. (? = 3 alınız.)
Cevap: 24
9) Daire alanı = πr². Soruda π = 3 alınacak.
Alanlar küçükten büyüğe: 75, 108, 144.
Her dairenin yarıçapı:
r₁² = 75/3 = 25 → r₁ = 5.
r₂² = 108/3 = 36 → r₂ = 6.
r₃² = 144/3 = 48 → r₃ = √48 ≈ 6.928.
Çemberler sıralı ve birbirine dokunacak şekilde yerleştirildiğine göre
A ile C arasındaki mesafe = (r₁ + r₂) + (r₂ + r₃) = r₁ + 2r₂ + r₃.
Bunu hesaplayalım: 5 + 2 · 6 + √48 = 5 + 12 + 6.928 ≈ 23.928.
En yakın doğal sayı 24’tür.
10) 1bc üç basamaklı ve 1c iki basamaklı doğal sayıdır. √1 bc + √1c işleminin sonucu tam sayıdır. Buna göre √b+c ifadesinin değerinin hangi tam sayıya daha yakın olduğunu bulunuz.
Cevap: 4
Verilen: 1bc üç basamaklı ve 1c iki basamaklı,
√1bc + √1c bir tam sayıdır. (Burada 1bc yüzler basamağı 1, onluk b, birler c; 1c = 10 + c.)
İki basamaklı 1c için tam kare olabilecekler: 16, 25, 36, 49, 64, 81. Sadece 16 biçimi “1c” ile uyumlu (c = 6).
Dolayısıyla 1c = 16 ve c = 6 olmalı (çünkü √1c tam sayı olursa toplamın tam sayı olması kolaylaşır).
Üç basamaklı 1bc tam kare olabilecekler (100–199 arası tam kareler): 100, 121, 144, 169, 196.
Bunların birler basamağı c olmalı; c = 6 olduğu için uygun olan 196 (yüzde 1, onluk b=9, birler 6).
Böylece 1bc = 196 ve √196 = 14, √16 = 4 ve toplam 18 (tam sayı) olur — koşul sağlanır.
Bulduğumuz b = 9, c = 6 ise b + c = 15.
√b + c = √15 ≈ 3.873 → en yakın tam sayı 4.












