8. Sınıf Matematik Ders Kitabı Sayfa 70-72. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 70-72. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 70-71-72 konularına ait cevapları bulabilirsiniz. “Kareköklü Bir İfadeyi a b Şeklinde Yazma ve a b Şeklindeki İfadede Katsayıyı Kök İçine Alma Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 70-72. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Kareköklü Bir İfadeyi a b Şeklinde Yazma ve a b Şeklindeki İfadede Katsayıyı Kök İçine Alma Cevapları
2. Ünite Kareköklü İfadeler: Kareköklü ifadelerde sayılar, kare sayılarla çarpılarak sadeleştirilebilir veya katsayılar karekök içine alınabilir. Bu işlemler, matematiksel ifadeleri daha basit ve anlaşılır hale getirir.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 70 Cevapları Sonuç Yayınları
Arda Bey ve Sibel Hanım aynı atölyede çalışıyor.
Arda Bey 7·√81 işleminin sonucu kadar,
Sibel Hanım ise 21·√9 işleminin sonucu kadar bardak üretiyor.
Arda Bey ile Sibel Hanım aynı sayıda bardak üretmiş olabilirler mi? Açıklayınız.
Cevap:
Evet, Arda Bey ile Sibel Hanım aynı sayıda bardak üretmiş olabilirler.
Bunu anlamak için her iki kişinin ürettiği bardak sayısını ayrı ayrı hesaplayalım.
Arda Bey’in ürettiği bardak sayısı:
İşlem: 7 · √81
Öncelikle karekök içindeki sayıyı hesaplarız: √81 = 9 (çünkü 9 · 9 = 81)
Şimdi bu sonucu 7 ile çarparız: 7 · 9 = 63
Arda Bey 63 adet bardak üretmiştir.
Sibel Hanım’ın ürettiği bardak sayısı:
İşlem: 21 · √9
Öncelikle karekök içindeki sayıyı hesaplarız: √9 = 3 (çünkü 3 · 3 = 9)
Şimdi bu sonucu 21 ile çarparız: 21 · 3 = 63
Sibel Hanım 63 adet bardak üretmiştir.
Sonuç: Her iki kişinin ürettiği bardak sayısı 63 olarak bulunmuştur. Bu nedenle Arda Bey ve Sibel Hanım aynı sayıda bardak üretmişlerdir.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 72 Cevapları Sonuç Yayınları
Alıştırmalar
1. Aşağıdaki ifadeleri a√b (a ≠ 1) şeklinde yazınız.
Cevap:
Bu sorularda karekök içindeki sayıyı, bir kare sayı ile başka bir sayının çarpımı şeklinde yazacağız. Daha sonra karekökün içinden kare sayıyı çıkaracağız.
a) √75
75 sayısını 25 · 3 olarak yazarız. (25 bir kare sayıdır, 5² = 25)
√75 = √(25 · 3)
√(25 · 3) = √25 · √3 = 5√3
Sonuç: 5√3
b) √250
250 sayısını 25 · 10 olarak yazarız.
√250 = √(25 · 10)
√(25 · 10) = √25 · √10 = 5√10
Sonuç: 5√10
c) √147
147 sayısını 49 · 3 olarak yazarız. (49 bir kare sayıdır, 7² = 49)
√147 = √(49 · 3)
√(49 · 3) = √49 · √3 = 7√3
Sonuç: 7√3
ç) √128
128 sayısını 64 · 2 olarak yazarız. (64 bir kare sayıdır, 8² = 64)
√128 = √(64 · 2)
√(64 · 2) = √64 · √2 = 8√2
Sonuç: 8√2
d) √52
52 sayısını 4 · 13 olarak yazarız. (4 bir kare sayıdır, 2² = 4)
√52 = √(4 · 13)
√(4 · 13) = √4 · √13 = 2√13
Sonuç: 2√13
e) √325
325 sayısını 25 · 13 olarak yazarız.
√325 = √(25 · 13)
√(25 · 13) = √25 · √13 = 5√13
Sonuç: 5√13
f) √968
968 sayısını 484 · 2 olarak yazarız. (484 bir kare sayıdır, 22² = 484)
√968 = √(484 · 2)
√(484 · 2) = √484 · √2 = 22√2
Sonuç: 22√2
g) √450
450 sayısını 225 · 2 olarak yazarız. (225 bir kare sayıdır, 15² = 225)
√450 = √(225 · 2)
√(225 · 2) = √225 · √2 = 15√2
Sonuç: 15√2
2. a√b şeklinde verilen aşağıdaki ifadelerde katsayıları kareköklerin içine alınız.
Cevap:
Bu sorularda katsayıyı (a) karekök içine almak için önce katsayının karesini alırız, sonra bu değeri karekök içindeki sayı (b) ile çarparız.
a) 3√7
Katsayının karesi: 3² = 9
Karekök içindeki sayı ile çarpımı: 9 · 7 = 63
Sonuç: √63
b) 7√14
Katsayının karesi: 7² = 49
Karekök içindeki sayı ile çarpımı: 49 · 14 = 686
Sonuç: √68
c) 3√5
Katsayının karesi: 3² = 9
Karekök içindeki sayı ile çarpımı: 9 · 5 = 45
Sonuç: √45
ç) 21√3
Katsayının karesi: 21² = 441
Karekök içindeki sayı ile çarpımı: 441 · 3 = 1323
Sonuç: √132
d) 8√2
Katsayının karesi: 8² = 64
Karekök içindeki sayı ile çarpımı: 64 · 2 = 128
Sonuç: √128
e) 3√15
Katsayının karesi: 3² = 9
Karekök içindeki sayı ile çarpımı: 9 · 15 = 135
Sonuç: √135
f) 10√17
Katsayının karesi: 10² = 100
Karekök içindeki sayı ile çarpımı: 100 · 17 = 1700
Sonuç: √1700
g) 5√5
Katsayının karesi: 5² = 25
Karekök içindeki sayı ile çarpımı: 25 · 5 = 125
Sonuç: √125
3. Aşağıdaki kareköklü ifadelerden değerleri eşit olanlar eşleştirildiğinde açıkta kalan kareköklü ifadeyi bulunuz.
Cevap:

Verilenler: √27, √40, √98, √128, √180, √147
Eşleştirme için sağdaki formlar: 3√3, 7√3, 8√2, 7√2, 6√5
Eşleştirmeler:
- √27 = √(9·3) = 3√3
- √147 = √(49·3) = 7√3
- √128 = √(64·2) = 8√2
- √98 = √(49·2) = 7√2
- √180 = √(36·5) = 6√5
Açıkta kalan: √40 (hiçbir verilen sağ ifadeyle eşleşmiyor)
4. Aşağıdaki eşitlikler doğru ise ilgili kutucuğa “D”, yanlış ise “Y” yazınız.
Cevap:
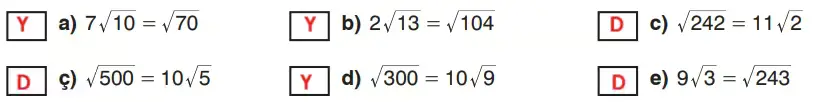
a) 7√10 = √70
Sol tarafı karekök içine alalım: 7√10 = √(7² · 10) = √(49 · 10) = √490
Eşitlik √490 = √70 olur. Bu ifade yanlıştır.
b) 2√13 = √104
Sol tarafı karekök içine alalım: 2√13 = √(2² · 13) = √(4 · 13) = √104
Eşitlik √104 = √104 olur. Bu ifade doğrudur.
c) √242 = 11√2
Sol tarafı sadeleştirelim: √242 = √(121 · 2) = √121 · √2 = 11√2
Eşitlik 11√2 = 11√2 olur. Bu ifade doğrudur.
ç) √500 = 10√5
Sol tarafı sadeleştirelim: √500 = √(100 · 5) = √100 · √5 = 10√5
Eşitlik 10√5 = 10√5 olur. Bu ifade doğrudur.
d) √300 = 10√9
Sol tarafı sadeleştirelim: √300 = √(100 · 3) = 10√3
Sağ tarafı sadeleştirelim: 10√9 = 10 · 3 = 30
Eşitlik 10√3 = 30 olur. Bu ifade yanlıştır.
e) 9√3 = √243
Sol tarafı karekök içine alalım: 9√3 = √(9² · 3) = √(81 · 3) = √243
Eşitlik √243 = √243 olur. Bu ifade doğrudur.