8. Sınıf Matematik Ders Kitabı Sayfa 73-78. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 73-78. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 73-74-75-76-77-7 konularına ait cevapları bulabilirsiniz. “Kareköklü İfadelerde Çarpma ve Bölme İşlemleri Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 73-78. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Kareköklü İfadelerde Çarpma ve Bölme İşlemleri Cevapları
2. Ünite Kareköklü İfadeler: Köklü ifadelerle yapılan çarpma ve bölme işlemlerinde, kök içindeki sayıların çarpanlarına ayrılması ve sadeleştirilmesi gerekir. Dik üçgenlerin alanı ise dik kenarların çarpımının yarısı formülüyle kolayca bulunabilir.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 73 Cevapları Sonuç Yayınları
Emir Bey, banyosunun dikdörtgen şeklindeki tabanını kenar uzunlukları √400 cm ve √900 cm olan dikdörtgen şeklindeki karolarla döşetiyor. Emir Bey, banyosunun tabanına 200 adet karo döşettiğine göre Emir Bey’in banyosunun taban alanı bulunurken nasıl bir yol izlenmelidir? Açıklayınız.
Cevap:
Öncelikle bir karonun alanını hesaplamalıyız:
Bir karonun alanı = √400 cm × √900 cm = 20 cm × 30 cm = 600 cm²
Emir Bey banyosuna 200 adet karo döşemiştir, bu nedenle banyosunun taban alanı:
Banyo taban alanı = Bir karonun alanı × Karo sayısı = 600 cm² × 200 = 120.000 cm²
Sonuç: 120000 cm² = 12 m².
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 78 Cevapları Sonuç Yayınları
1. Yandaki KLM dik üçgeninde KL = 6 cm, LM = 6√3 cm’dir.
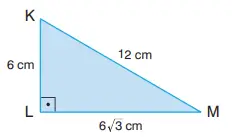
Buna göre KLM dik üçgeninin alanı kaç cm²’dir?
Cevap:
KLM dik üçgeninde L noktasında dik açı bulunmaktadır. Dik üçgenin alanı, dik kenarların çarpımının yarısıdır.
Alan = (KL × LM) / 2
Alan = (6 cm × 6√3 cm) / 2
Alan = 36√3 cm² / 2
Alan = 18√3 cm²
Bu nedenle, KLM dik üçgeninin alanı 18√3 cm²’dir.
2. Aşağıdaki çarpma işlemlerini yapınız.
Cevap:
a) 3√5 · 5√7 · 7 · √35
Sayısal katsayıları çarp: 3·5·7 = 105.
Kök içlerini birleştir: √(5·7·35).
5·7·35 = 5·7·(5·7) = (5·5)·(7·7) = 25·49.
√(25·49) = 5·7 = 35.
Sonuç: 105 · 35 = 3675.
b) √50 · √20
Birleştir: √(50·20) = √1000.
1000 = 100·10, dolayısıyla √1000 = √(100·10) = 10√10.
Cevap: 10√10
c) √80 · (3/5 · √5)
Kökleri birleştir: √80 · √5 = √(80·5) = √400.
√400 = 20.
Katsayı ile çarp: (3/5) · 20 = 3·4 = 12.
Sonuç: 12
ç) √18 · 3√2 · 7 · √3
Sayısal katsayıları ayır: 3·7 = 21.
Kökleri birleştir: √(18·2·3) = √(18·6) = √108.
√108 = √(36·3) = 6√3.
Sonuç: 21 · 6√3 = 126√3.
d) 3√7 · √343
√343 = √(49·7) = 7√7.
3√7 · 7√7 = 3·7 · (√7·√7) = 21 · 7 = 147.
Cevap: 147
e) √3 · (7/3 · √27)
√27 = √(9·3) = 3√3.
(7/3) · √27 = (7/3) · 3√3 = 7√3.
√3 · 7√3 = 7 · (√3·√3) = 7·3 = 21.
Sonuç: 21
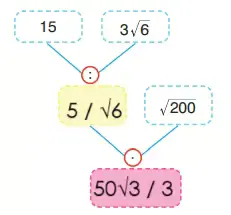
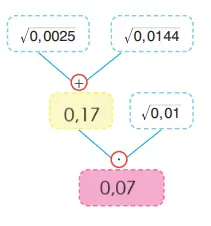
3. Yandaki şemada belirtilen işlemleri yaparak renkli kutucuklara cevapları yazınız.
Cevap:
Şemadaki işlemi adım adım çözelim:
15 ÷ (3√6) = 15 / (3√6) = 5 / √6
(5 / √6) · √200 = 5 · √(200 / 6) = 5 · √(100 / 3) = 5 · (10 / √3) = 50 / √3
Rasyonelleştirme:
(50 / √3) · (√3 / √3) = (50√3) / 3
Bu nedenle, renkli kutucuklara yazılacak cevaplar:
Sarı kutu = 5 / √6
Pembe kutu = 50√3 / 3
4. Aşağıdaki işlemleri yapınız.
Cevap:
a) (6√2 · √48) / (8√6)
→ √48 = 4√3
→ Üst: 6√2 · 4√3 = 24√6
→ 24√6 / 8√6 = 24 / 8 = 3
b) (√70 · √14) / √5
→ √(70 · 14 / 5) = √(980 / 5) = √196 = 14
c) (6√2) / (3√6) · √3
→ 6√2 / 3√6 = 2√(2 / 6) = 2 / √3
→ (2 / √3) · √3 = 2
ç) (10√2 · 2√10) / (2√5)
→ Üst: 20√20
→ 20√20 / 2√5 = 10√(20 / 5) = 10√4 = 20
d) (√18 · √27 · √72) / √300
→ √18 = 3√2, √27 = 3√3, √72 = 6√2
→ Üst: 3√2 · 3√3 · 6√2 = 54√12 = 108√3
→ √300 = 10√3
→ 108√3 / 10√3 = 108 / 10 = 54 / 5 = 10,8
e) (12√18) / (8√3)
→ √18 = 3√2
→ Üst: 12 · 3√2 = 36√2
→ 36√2 / 8√3 = (9√2) / (2√3) = (9√6) / 6 = 3√6 / 2