8. Sınıf Matematik Ders Kitabı Sayfa 79-84-85. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 79-84-85. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 79-80-81-82-83-84-85 konularına ait cevapları bulabilirsiniz. “Kareköklü İfadelerde Toplama ve Çıkarma İşlemleri Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 79-84-85. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Kareköklü İfadelerde Toplama ve Çıkarma İşlemleri Etkinlik Cevapları
2. Ünite Kareköklü İfadeler: Kareköklü ifadelerde toplama ve çıkarma işlemleri yaparken benli terimler birleştirilir. Kök içindeki sayılar sadeleştirilerek işlemler kolaylaştırılır ve sonuçlar basit hale getirilir.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 79 Cevapları Sonuç Yayınları
Güneş, iki aşamadan oluşan bir koşu yarışına katılıyor. Koşu yarışında yarışçıların birinci aşamada √1800 m uzunluğundaki parkuru, ikinci aşamada ise √3200 m uzunluğundaki parkuru koşmaları gerekiyor. Güneş yarışta birinci aşamayı tamamlıyor. İkinci aşamada ise parkurda √2450 m’lik uzunluğu koşuyor. Buna göre Güneş’in yarışı tamamlayabilmesi için koşması gereken yol miktarı bulunurken hangi işlemler yapılmalıdır? Açıklayınız.
Cevap:
Adım 1: toplam yarış mesafesini ve koşulan mesafeyi ifade edelim
toplam mesafe = (1. aşama) + (2. aşama) = √1800 + √3200
koşulan mesafe = (1. aşama) + (2. aşamanın koşulan kısmı) = √1800 + √2450
Adım 2: kalan mesafeyi bulmak için işlemi kuralım
kalan mesafe = toplam mesafe − koşulan mesafe
kalan mesafe = (√1800 + √3200) − (√1800 + √2450)
Adım 3: işlemi basitleştirelim
parantezi açalım: √1800 + √3200 − √1800 − √2450
√1800 terimleri birbirini götürür.
kalan mesafe = √3200 − √2450
Adım 4: kök ifadeleri sadeleştirip işlemi sonuçlandıralım
√3200 = √(64 × 50) = √64 × √50 = 8√50
√2450 = √(49 × 50) = √49 × √50 = 7√50
kalan mesafe = 8√50 − 7√50
kalan mesafe = (8 − 7)√50 = 1√50
Güneş’in yarışı tamamlayabilmesi için koşması gereken yol √50 metre‘dir.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 84 Cevapları Sonuç Yayınları
1. Aşağıdaki işlemlerin sonuçlarını bulunuz.
Cevap:
a) √32 − 5√2 + 6√2 =
√32’yi sadeleştirelim: √32 = √(16 × 2) = √16 × √2 = 4√2
İşlemi güncelleyelim: 4√2 − 5√2 + 6√2
Benli terimleri toplayalım: (4 − 5 + 6)√2 = 5√2
Sonuç: 5√2
b) √700 + 3√7 =
√700’ü sadeleştirelim: √700 = √(100 × 7) = √100 × √7 = 10√7
İşlemi güncelleyelim: 10√7 + 3√7
Benli terimleri toplayalım: (10 + 3)√7 = 13√7
Sonuç: 13√7
c) √15 − √1500 + 20√15 =
√1500’ü sadeleştirelim: √1500 = √(100 × 15) = √100 × √15 = 10√15
İşlemi güncelleyelim: √15 − 10√15 + 20√15
Benli terimleri toplayalım: (1 − 10 + 20)√15 = 11√15
Sonuç: 11√15
ç) (√2 / √3) · (7√6 − √24) =
Önce parantez içini sadeleştirelim: √24 = √(4 × 6) = √4 × √6 = 2√6
Parantez içi yeni hali: 7√6 − 2√6 = 5√6
İşlemi güncelleyelim: (√2 / √3) · 5√6
Köklü ifadeleri çarpalım: (√2 × 5√6) / √3 = (5 × √12) / √3
√12’yi sadeleştirelim: √12 = √(4 × 3) = √4 × √3 = 2√3
İşlemi güncelleyelim: (5 × 2√3) / √3 = 10√3 / √3
Sadeleştirelim: 10
Sonuç: 10
d) 7√5 − √5 − √180 =
√180’ı sadeleştirelim: √180 = √(36 × 5) = √36 × √5 = 6√5
İşlemi güncelleyelim: 7√5 − √5 − 6√5
Benli terimleri toplayalım: (7 − 1 − 6)√5 = 0√5
Sonuç: 0
e) −(25√10 + √10) + 6√10 =
Parantezi açalım: −25√10 − √10 + 6√10
Benli terimleri toplayalım: (−25 − 1 + 6)√10 = −20√10
Sonuç: −20√10
2. Aşağıdaki işlemler ile işlemlerin sonuçları eşleştirildiğinde hangi ifade açıkta kalır?
Cevap:
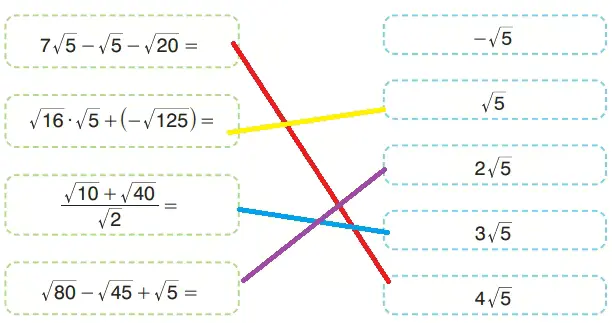
1. İşlem: 7√5 – √5 – √20
Öncelikle karmaşık kökü sadeleştirelim: √20 = √(4 × 5) = √4 × √5 = 2√5
Bu değeri işlemin yerine yazalım: 7√5 – √5 – 2√5
Şimdi benli terimleri (kök içindei 5 olanları) toplayalım: (7 – 1 – 2)√5 = 4√5
Sonuç: 4√5
2. İşlem: √16 · √5 + (−√125)
Köklü ifadeleri sadeleştirelim:
√16 = 4
√125 = √(25 × 5) = √25 × √5 = 5√5
Bu değerleri işlemin yerine yazalım: 4 · √5 – 5√5
İşlemi düzenleyelim: 4√5 – 5√5
Benli terimleri toplayalım: (4 – 5)√5 = -√5
Sonuç: -√5
3. İşlem: (√10 + √40) / √2
Öncelikle paydaki karmaşık kökü sadeleştirelim: √40 = √(4 × 10) = √4 × √10 = 2√10
Bu değeri işlemin yerine yazalım: (√10 + 2√10) / √2
Paydaki benli terimleri toplayalım: (1 + 2)√10 = 3√10
İşlem yeni haliyle: 3√10 / √2
Kökleri bölelim: 3 · (√10 / √2) = 3 · √(10/2) = 3 · √5 = 3√5
* Sonuç: 3√5
4. İşlem: √80 – √45 + √5
Karmaşık kökleri sadeleştirelim:
√80 = √(16 × 5) = √16 × √5 = 4√5
√45 = √(9 × 5) = √9 × √5 = 3√5
Bu değerleri işlemin yerine yazalım: 4√5 – 3√5 + √5
Benli terimleri toplayalım: (4 – 3 + 1)√5 = 2√5
Sonuç: 2√5
Eşleştirmeler:
7√5 – √5 – √20 → 4√5
√16·√5 + (−√125) → -√5
(√10 + √40)/√2 → 3√5
√80 – √45 + √5 → 2√5
Açıkta kalan ifade: √5
(√288 − √32) / (√36 · √8) işleminin sonucunu bulunuz.
Cevap:
√288 = √(144×2) = 12√2
√32 = √(16×2) = 4√2
√36 = 6
√8 = 2√2
İşlem:
(12√2 − 4√2) / (6 · 2√2)
Üst: 8√2
Alt: 12√2
(8√2) / (12√2) = 8 / 12 = 2 / 3
Sonuç: 2 / 3
8. Sınıf Matematik Ders Kitabı Sayfa 85 Cevapları Sonuç Yayınları
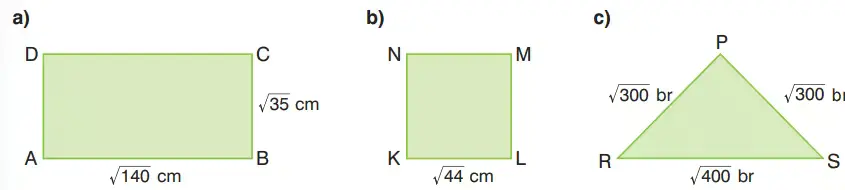
4. Aşağıda kenar uzunlukları verilen dikdörtgen, kare ve üçgenin çevre uzunluklarını bulunuz.
Cevap:
a) Dikdörtgen ABCD
Verilenler:
AB = √140 cm
BC = √35 cm
Hatırlatma: Dikdörtgende karşılıklı kenarlar eşittir.
AB = CD = √140 cm
BC = AD = √35 cm
Çevre Formülü: Çevre = 2 × (Uzun kenar + Kısa kenar)
İşlem:
Çevre = 2 × (AB + BC)
Çevre = 2 × (√140 + √35)
Sadeleştirme: √140 ifadesini √35 cinsinden ifade edebiliriz.
√140 = √(4 × 35) = √4 × √35 = 2√35
İşlemi Güncelleme:
Çevre = 2 × (2√35 + √35)
Parantez içini toplayalım: 2 × (3√35)
Çevre = 6√35 cm
Sonuç: Dikdörtgenin çevre uzunluğu 6√35 cm’dir.
b) Kare KLMN
Verilen:
Bir kenar = √44 cm
Hatırlatma: Karenin dört kenarı da eşittir.
Çevre Formülü: Çevre = 4 × Kenar
İşlem:
Çevre = 4 × √44
Sadeleştirme: √44 ifadesini sadeleştirelim.
√44 = √(4 × 11) = √4 × √11 = 2√11
İşlemi Güncelleme:
Çevre = 4 × 2√11
Çevre = 8√11 cm
Sonuç: Karenin çevre uzunluğu 8√11 cm’dir.
c) Üçgen PRS
Verilenler:
Kenarlar = √300 br, √300 br, √400 br
Hatırlatma: Üçgenin çevresi, üç kenarın uzunluklarının toplamıdır.
Çevre Formülü: Çevre = Kenar₁ + Kenar₂ + Kenar₃
İşlem:
Çevre = √300 + √300 + √400
Sadeleştirme: Köklü ifadeleri sadeleştirelim.
√300 = √(100 × 3) = √100 × √3 = 10√3
√400 = √(100 × 4) = √100 × √4 = 10 × 2 = 20
İşlemi Güncelleme:
Çevre = 10√3 + 10√3 + 20
Benli terimleri toplayalım: (10 + 10)√3 + 20
Çevre = 20√3 + 20 br
(İsterseniz faktör çıkarabilirsiniz: 20(√3 + 1) br. Her iki cevap da doğrudur.)
Sonuç: Üçgenin çevre uzunluğu 20√3 + 20 br’dir.
5. Yandaki tabloda bazı işlemler verilmiştir. İşlemleri yaparak tablodaki boş kutucuklara işlemlerin sonuçlarını yazınız.
Cevap:
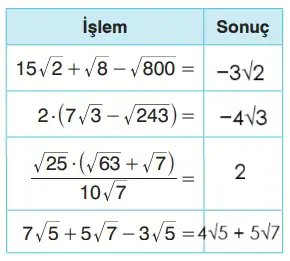
15√2 + √8 − √800
√8 = 2√2, √800 = √(400×2) = 20√2
→ 15√2 + 2√2 − 20√2 = (15 + 2 − 20)√2 = −3√2
2 · (7√3 − √243)
√243 = √(81×3) = 9√3
→ 2 · (7√3 − 9√3) = 2 · (−2√3) = −4√3
(√25 · (√63 + √7)) / (10√7)
√25 = 5, √63 = √(9×7) = 3√7
→ (5 · (3√7 + √7)) / (10√7) = (5 · 4√7) / (10√7) = (20√7) / (10√7) = 2
7√5 + 5√7 − 3√5
Benzer köklü terimleri birleştirelim:
(7√5 − 3√5) + 5√7 = 4√5 + 5√7
Sonuç: 4√5 + 5√7
6. Yukarıda verilen şemadaki ifadeleri en soldan başlayarak inceleyiniz. İfadeler doğru ise “D”, yanlış ise “Y” yolunu takip ediniz. Kaçıncı çıkışa ulaştınız? Yazınız.
Cevap:
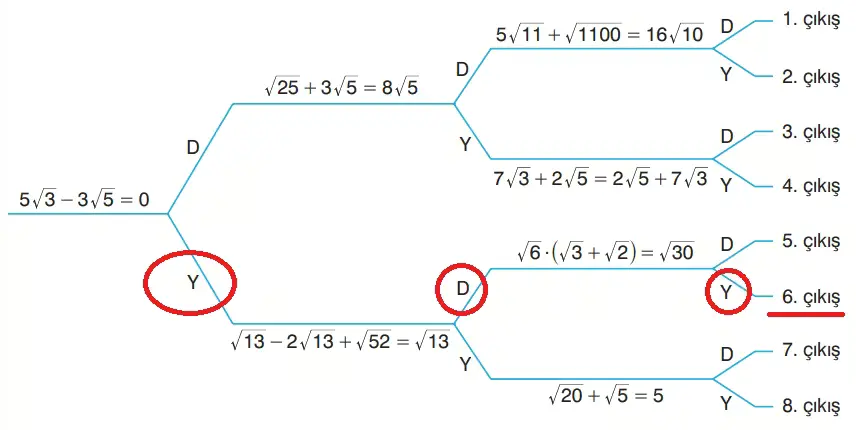
Başlangıç İfadesi
5√3 − 3√5 = 0
Bu ifade yanlıştır, çünkü kök içleri farklı (√3 ≠ √5).
→ Y yolunu izliyoruz.
(Y Yolundaki İfade)
√13 − 2√13 + √52 = √13
√52 = 2√13 olduğundan:
√13 − 2√13 + 2√13 = √13
→ Doğru (D) yolunu izliyoruz.
(D Yolundaki İfade)
√6 · (√3 + √2) = √30
Dağıtalım:
√6·√3 + √6·√2 = √18 + √12 = 3√2 + 2√3 ≠ √30
→ Yanlış (Y) yolunu izliyoruz.
Sonuç: Bu “Y” dalı bizi 6. çıkışa götürür.