8. Sınıf Matematik Ders Kitabı Sayfa 80-82-83-84-85-86. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 80-82-83-84-85-86. Cevapları MEB Yayınları bölümünde, ders kitabı sayfa 80-81-82-83-84-85-86 konularına ait cevapları bulabilirsiniz. “Kareköklü İfadelerde Toplama ve Çıkarma İşlemi Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 80-82-83-84-85-86. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Kareköklü İfadelerde Toplama ve Çıkarma İşlemi Cevapları
2. Ünite 1. Bölüm Kareköklü İfadeler: Kareköklü ifadelerde benzer köklü terimler birleştirilerek sadeleştirme yapılır. Farklı köklü ifadeler ise sadeleştirilemez ve kendi halinde bırakılır.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 80 Cevapları MEB Yayınları

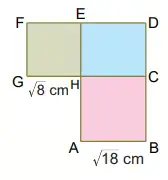
Tayfun, alanı 20 metrekare olan kare şeklindeki bahçesinde 4 çeşit ürün yetiştirmek istiyor. Bahçesini 4 eşit kare biçiminde parçalara ayırıyor.
Kare biçimindeki bölgelerin kenar uzunluğunu herhangi bir tam sayının karekökü olarak ifade edebilir miyiz?
Cevap: Her bir küçük karenin alanı 20/4 = 5 m² olacaktır. Bu küçük karenin kenar uzunluğu √5 m’dir. √5 herhangi bir tam sayının karekökü olarak ifade edilemez, çünkü 5 asal sayıdır ve tam kare değildir.
Her bir ürünün yetiştirildiği karesel bölgelerin kenar uzunluklarından yararlanarak bu bahçenin bir kenar uzunluğunu nasıl ifade edebiliriz?
Cevap: Büyük karenin alanı 20 m² olduğundan, bir kenar uzunluğu √20 m’dir. √20 = √(4×5) = 2√5 m olarak ifade edilebilir. Aynı zamanda, küçük karenin kenarı √5 m olduğundan, büyük karenin bir kenarı 2√5 m olarak da ifade edilebilir. Bu, küçük karenin kenar uzunluğunun 2 katına eşittir.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 82 Cevapları MEB Yayınları
Sıra Sizde 1
Aşağıdaki işlemleri yapınız.
Cevap:
a) 7√2 + 11√2 = (7 + 11)√2 = 18√2
b) 7√3 – 8√3 = (7 – 8)√3 = -√3
c) 2√13 + 6√13 – 9√13 = (2 + 6 – 9)√13 = -√13
ç) 6√8 – 15√8 + 3√8 = (6 – 15 + 3)√8 = -6√8
√8 = √(4×2) = 2√2 olduğundan: -6√8 = -6 × 2√2 = -12√2
d) 21√12 – 5√27 = 21 × √(4×3) – 5 × √(9×3) = 21 × 2√3 – 5 × 3√3 = 42√3 – 15√3 = (42 – 15)√3 = 27√3
e) 5√63 – 2√28 = 5 × √(9×7) – 2 × √(4×7) = 5 × 3√7 – 2 × 2√7 = 15√7 – 4√7 = (15 – 4)√7 = 11√7
Sıra Sizde 2
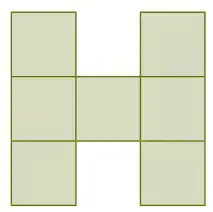
Yandaki şekil her birinin alanı 52 cm2 olan eş karelerden oluşmuştur.
Buna göre şeklin çevresini santimetre cinsinden bulunuz.
Cevap:
Her bir karenin alanı 52 cm² olduğundan, bir kenar uzunluğu √52 cm’dir.
√52 = √(4×13) = 2√13 cm bulunur.
Şekilde 7 adet kare bulunmaktadır ve bu karelerden oluşan şeklin dışta kalan kenarlarının toplam uzunluğu (çevre) 16 adet küçük kenara eşittir.
Bu nedenle şeklin çevresi = 16 × 2√13 = 32√13 cm’dir.
8. Sınıf Matematik Ders Kitabı Sayfa 83 Cevapları MEB Yayınları
Sıra Sizde 3
Aşağıdaki kareköklü ifadelerle çarpıldığında sonucu doğal sayı yapan birer çarpan bulunuz.
Cevap:
a) 5√8 için çarpan: √2
√8 × √2 = √16 = 4 (doğal sayı)
5√8 × √2 = 5 × 4 = 20 (doğal sayı)
b) 2√20 için çarpan: √5
√20 × √5 = √100 = 10 (doğal sayı)
2√20 × √5 = 2 × 10 = 20 (doğal sayı)
c) √68 için çarpan: √17
√68 × √17 = √(68×17) = √1156 = 34 (doğal sayı)
8. Sınıf Matematik Ders Kitabı Sayfa 84 Cevapları MEB Yayınları
Düşünme Zamanı
Aşağıdaki prizmaları zemin üzerinde yüzeyleri çakışacak şekilde üst üste koyarak istenen yüksekliklerde kuleler yapılacaktır.
Her prizmadan yeteri kadar bulunduğuna göre her kulede kullanılması gereken prizma sayısının en az kaç olabileceğini belirleyiniz?
Cevap:
a) İstenen Yükseklik: √2700 = 30√3 br
Prizma Yükseklikleri: √243 = 9√3 br, √147 = 7√3 br, √48 = 4√3 br
Hesaplamalar:
30√3 / 9√3 = 3.33 → 4 prizma
30√3 / 7√3 = 4.29 → 5 prizma
30√3 / 4√3 = 7.5 → 8 prizma
Sonuç: En az 4 prizma.
b) İstenen Yükseklik: √3200 = 40√2 br
Prizma Yükseklikleri: √162 = 9√2 br, √98 = 7√2 br, 50 br
Hesaplamalar:
40√2 / 9√2 = 4.44 → 5 prizma
40√2 / 7√2 = 5.71 → 6 prizma
40√2 / 50 ≈ 1.13 → 2 prizma
Sonuç: En az 2 prizma.
c) İstenen Yükseklik: √3750 = 25√6 br
Prizma Yükseklikleri: √384 = 8√6 br, 294 br, 54 br
Hesaplamalar:
25√6 / 8√6 = 3.125 → 4 prizma
25√6 / 294 ≈ 0.21 → 1 prizma
25√6 / 54 ≈ 1.13 → 2 prizma
Sonuç: En az 1 prizma.
ç) İstenen Yükseklik: √5120 = 32√5 br
Prizma Yükseklikleri: √245 = 7√5 br, √180 = 6√5 br, √125 = 5√5 br
Hesaplamalar:
32√5 / 7√5 = 4.57 → 5 prizma
32√5 / 6√5 = 5.33 → 6 prizma
32√5 / 5√5 = 6.4 → 7 prizma
Sonuç: En az 5 prizma.
8. Sınıf Matematik Ders Kitabı Sayfa 85 Cevapları MEB Yayınları
Alıştırmalar Cevapları
1 Aşağıdaki işlemleri yapınız.
Cevap:
a) √27 + 5√3 – √12 = √(9×3) + 5√3 – √(4×3) = 3√3 + 5√3 – 2√3 = (3 + 5 – 2)√3 = 6√3
b) 7√125 – 11√5 + √45 = 7√(25×5) – 11√5 + √(9×5) = 7×5√5 – 11√5 + 3√5 = 35√5 – 11√5 + 3√5 = (35 – 11 + 3)√5 = 27√5
c) 5√8 + 2√800 – 9√200 = 5√(4×2) + 2√(400×2) – 9√(100×2) = 5×2√2 + 2×20√2 – 9×10√2 = 10√2 + 40√2 – 90√2 = (10 + 40 – 90)√2 = -40√2
ç) 7√72 – 10√32 + 3√8 = 7√(36×2) – 10√(16×2) + 3√(4×2) = 7×6√2 – 10×4√2 + 3×2√2 = 42√2 – 40√2 + 6√2 = (42 – 40 + 6)√2 = 8√2
d) 21√12 – 5√27
√12 = √(4×3) = 2√3
√27 = √(9×3) = 3√3
21√12 – 5√27 = 21 × 2√3 – 5 × 3√3 = 42√3 – 15√3 = (42 – 15)√3 = 27√3
e) 5√99 – 2√44 + 3√176
√99 = √(9×11) = 3√11
√44 = √(4×11) = 2√11
√176 = √(16×11) = 4√11
5√99 – 2√44 + 3√176 = 5 × 3√11 – 2 × 2√11 + 3 × 4√11 = 15√11 – 4√11 + 12√11 = (15 – 4 + 12)√11 = 23√11
2 Aşağıdaki kareköklü ifadelerle çarpıldığında sonucu doğal sayı yapacak birer çarpan bulunuz.
Cevap:
a) √18 için çarpan: √2
√18 × √2 = √36 = 6 (doğal sayı)
b) √28 için çarpan: √7
√28 × √7 = √196 = 14 (doğal sayı)
c) √60 için çarpan: √15
√60 × √15 = √900 = 30 (doğal sayı)
ç) √75 için çarpan: √3
√75 × √3 = √225 = 15 (doğal sayı)
3. √29 − √18 − √7 − √9 işleminin sonucunu bulunuz.
Cevap:
İlk olarak √9 ifadesini sadeleştirelim:
√9 = 3 (çünkü 3² = 9)
√18 ifadesini sadeleştirelim:
√18 = √(9×2) = √9 × √2 = 3√2
Bu sadeleştirmeleri orijinal ifadeye yerleştirelim:
√29 − √18 − √7 − √9 = √29 − 3√2 − √7 − 3
İfadeyi düzenleyelim:
√29 − 3√2 − √7 − 3
Sonuç: Bu ifade daha fazla sadeleştirilemez, çünkü tüm kareköklü ifadeler (√29, √2 ve √7) farklıdır ve birbirleriyle toplanıp çıkarılamaz. Sadeleştirilebilecek tek parça √9 idi, bunu zaten 3 olarak sadeleştirdik.
Bu nedenle, işlemin sonucu: √29 − 3√2 − √7 − 3 şeklindedir.
4. √48 + √192 toplamının √12 sayısının kaç katı olduğunu bulunuz.
Cevap:
√48 + √192 = √(16×3) + √(64×3) = 4√3 + 8√3 = 12√3
√12 = √(4×3) = 2√3
Bölme işlemi: (12√3) / (2√3) = 6
Sonuç: √48 + √192 toplamı, √12 sayısının 6 katıdır.
5. A şehrinden ortalama sürati saatte √16000 km ve
B şehrinden ortalama sürati saatte √9000 km olan iki araç aynı anda aynı yöne doğru harekete geçiyor.
İki araç 5 saat sonra aynı anda C şehrine varıyor.
Buna göre A ile B şehirleri arasındaki mesafenin kaç kilometre olduğunu bulunuz.
Cevap:
A aracının hızı: √16000 km/saat
B aracının hızı: √9000 km/saat
Her iki araç 5 saat sonra C şehrine ulaştığına göre:
AC = 5 × √16000 km
BC = 5 × √9000 km
AB = AC – BC = 5 × √16000 – 5 × √9000 = 5 × (√16000 – √9000)
√16000 = √(1600×10) = 40√10
√9000 = √(900×10) = 30√10
AB = 5 × (40√10 – 30√10) = 5 × 10√10 = 50√10 km
8. Sınıf Matematik Ders Kitabı Sayfa 86 Cevapları MEB Yayınları
6. √2ᵃ + √2³ = 6√2 eşitliğinde a doğal sayısının değerini bulunuz.
Cevap:
√(2³) = √8 = √(4×2) = 2√2
Denklemin sol tarafı: √(2ᵃ) + 2√2 = 6√2
√(2ᵃ) = 6√2 – 2√2 = 4√2
Her iki tarafın karesini alalım:
(√(2ᵃ))² = (4√2)²
2ᵃ = 16 × 2
2ᵃ = 32
2ᵃ = 2⁵
Bu denklemden a = 5 bulunur.
7. √50 + √18 ifadesi ile √50 − √18 ifadesi arasındaki en büyük tam sayı ile en küçük tam sayı sayının farkını bulunuz.
Cevap:
√50 = √(25×2) = 5√2 ≈ 5 × 1.414 = 7.07
√18 = √(9×2) = 3√2 ≈ 3 × 1.414 = 4.24
√50 + √18 ≈ 7.07 + 4.24 = 11.31
Bu ifadeden küçük en büyük tam sayı: 11
√50 – √18 ≈ 7.07 – 4.24 = 2.83
Bu ifadeden büyük en küçük tam sayı: 3
Fark: 11 – 3 = 8
8. Alanları 128 ve 200 metrekare olan kare şeklindeki iki bahçenin çevreleri toplamını bulunuz.
Cevap:
Birinci karenin alanı: 128 m²
Birinci karenin kenar uzunluğu: √128 = √(64×2) = 8√2 m
Birinci karenin çevresi: 4 × 8√2 = 32√2 m
İkinci karenin alanı: 200 m²
İkinci karenin kenar uzunluğu: √200 = √(100×2) = 10√2 m
İkinci karenin çevresi: 4 × 10√2 = 40√2 m
Çevreler toplamı: 32√2 + 40√2 = 72√2 m
9. √12 + 2√12 + 3√12 + 4√12 toplamının √3 + 2√3 + 3√3 + 4√3 + 5√3 toplamından ne kadar fazla olduğunu bulunuz.
Cevap:
Öncelikle denklemdeki √(2³) ifadesini sadeleştirelim:
√(2³) = √8 = √(4×2) = √4 × √2 = 2√2
Bu değeri denkleminde yerine yazalım:
√(2ᵃ) + 2√2 = 6√2
√(2ᵃ) ifadesini yalnız bırakmak için 2√2’yi sağ tarafa atalım:
√(2ᵃ) = 6√2 – 2√2
√(2ᵃ) = 4√2
Her iki tarafın karesini alalım:
(√(2ᵃ))² = (4√2)²
2ᵃ = 16 × 2
2ᵃ = 32
32 sayısını 2’nin kuvveti olarak ifade edelim:
32 = 2⁵
Bu durumda:
2ᵃ = 2⁵
Tabanlar eşit olduğundan, üsler de eşit olmalıdır:
a = 5
Sonuç: a doğal sayısının değeri 5’tir.
10. Yukarıda kısa kenar uzunluğu √8 cm, uzun kenar uzunlukları sırasıyla √50 cm, √72 cm ve √98 cm olan paralelkenarlar verilmiştir.
Bu paralelkenarlar sırasıyla 2, 3 ve 5 eş parçaya ayrılmış, birer parçası Şekil 1’deki gibi kısa kenarları çakışık olacak şekilde birleştirilmiştir.
Cevap:
√8 = √(4×2) = 2√2 cm
√50 = √(25×2) = 5√2 cm
√72 = √(36×2) = 6√2 cm
√98 = √(49×2) = 7√2 cm
Paralelkenarların bölünmüş parçalarının uzunlukları:
Birinci paralelkenardan alınan parça: 5√2 / 2 = (5/2)√2 cm
İkinci paralelkenardan alınan parça: 6√2 / 3 = 2√2 cm
Üçüncü paralelkenardan alınan parça: 7√2 / 5 = (7/5)√2 cm
Birleştirilmiş şeklin uzun kenarlarının toplamı:
(5/2)√2 + 2√2 + (7/5)√2 = (5/2 + 2 + 7/5)√2 cm
Paydaları eşitleyelim: (5/2 + 4/2 + 7/5)√2 = (9/2 + 7/5)√2 = (45/10 + 14/10)√2 = (59/10)√2 cm
Birleştirilmiş şeklin kısa kenarı: 2√2 cm
Birleştirilmiş şeklin çevresi: 2 × (kısa kenar + uzun kenar) = 2 × (2√2 + (59/10)√2) cm
= 2 × (20/10√2 + 59/10√2) cm
= 2 × (79/10√2) cm
= (79/5)√2 cm