8. Sınıf Matematik Ders Kitabı Sayfa 86-88. Cevapları

8. Sınıf Matematik Ders Kitabı Sayfa 86-88. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 86-87-88 konularına ait cevapları bulabilirsiniz. “Kareköklü Bir İfade ile Çarpıldığında Sonucu Doğal Sayı Yapan Çarpanlar Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 86-88. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.

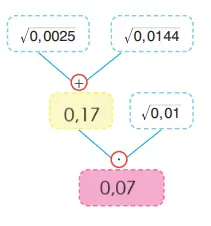
Kareköklü Bir İfade ile Çarpıldığında Sonucu Doğal Sayı Yapan Çarpanlar Cevapları

2. Ünite Kareköklü İfadeler: Kareköklü ifadelerin çarpımında doğal sayı elde etmek için, kök içindeki sayıların çarpımının tam kare olması gerekir. Bu durum, kök içindeki asal çarpanların çift üslü olmasını sağlayacak şekilde çarpanların seçilmesiyle mümkündür.

İçindekiler

8. Sınıf Matematik Ders Kitabı Sayfa 86 Cevapları Sonuç Yayınları

Bir belediye, bir parkın yanına dikdörtgen şeklinde yürüyüş yolu yapıyor. Yürüyüş yolunun uzun kenar uzunluğu 40√3 m ve alanı m² biriminde bir doğal sayıdır. Buna göre yürüyüş yolunun kısa kenar uzunluğu belirlenirken nasıl bir yol izlenebilir? Açıklayınız.
Cevap:

Uzun kenar L = 40√3 m, kısa kenar x m olsun.
Alan: A = L · x = 40√3 · x

A’nın doğal sayı olması için 40√3 · x ifadesindeki √3’ün etkisi yok olmalıdır.
Bunun için x = k·√3 (k ∈ ℕ) alınır.

O halde
A = 40√3 · (k√3) = 40 · 3 · k = 120k

Bu değer her k için doğal sayıdır.

Örnekler:
k = 1 ⇒ x = √3 m, A = 120 m²
k = 2 ⇒ x = 2√3 m, A = 240 m²

Not: Eğer alanın belli bir doğal sayı m olmasını istersek kısa kenar
x = m / (40√3) = (m√3) / 120 şeklinde verilir.

Farklı bir sayfa mı arıyorsunuz?

İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:

MEB Yayınları SONUÇ Yayıncılık Tüm Kitaplar

8. Sınıf Matematik Ders Kitabı Sayfa 88 Cevapları Sonuç Yayınları

Alıştırmalar

1. Aşağıdaki kareköklü ifadelerle çarpıldığında sonucu bir doğal sayı olan çarpanlara dörder örnek veriniz.
Cevap:

a) √120 → 120 = 4 × 30 → tam kare elde etmek için √30 ile çarpılır.
Örnek çarpanlar: √30, √480, √1080, √2700
(Çünkü: √120 × √30 = √3600 = 60)

b) √300 → 300 = 100 × 3 → tam kare elde etmek için √3 ile çarpılır.
Örnek çarpanlar: √3, √12, √27, √48
(√300 × √3 = √900 = 30)

c) 2√17 → sonucu doğal sayı yapmak için √17 ile çarpılır.
Örnek çarpanlar: √17, 2√17, 3√17, 4√17
(2√17 × √17 = 34)

ç) 5√19 → √19 ile çarpılırsa doğal sayı olur.
Örnek çarpanlar: √19, 2√19, 3√19, 4√19
(5√19 × √19 = 95)

2. Aşağıdaki işlemlerin sonuçları birer doğal sayıdır. Buna göre işlemlerdeki sembollerin yerine yazılabilecek en küçük pozitif tam sayıları belirleyiniz.
Cevap:

a) √88 · 9√△ = 9√(88×△)
Doğal sayı olması için 88×△ tam kare olmalı.
88 = 4×22 → kalan 22’yi tamamlamak için △ = 22 alınır.
Sonuç: △ = 22

b) √60 · 2√□ = 2√(60×□)
60 = 4×15 → kalan 15’i tamamlamak için □ = 15 alınır.
Sonuç: □ = 15

c) 7√◇ · √10 = 7√(◇×10)
◇×10 tam kare olmalı. En küçük tam kare 100 → ◇ = 10
Sonuç: ◇ = 10

ç) √324 · √▽ = √(324×▽)
324 = 18² → zaten tam kare → ▽ = 1
Sonuç: ▽ = 1

3. Yandaki UVYZ dikdörtgeninin alanı m² biriminde bir doğal sayıdır. Buna göre UVYZ dikdörtgeninin kısa kenar uzunluğunun metre biriminde alabileceği değerlere üç örnek veriniz.
(UV = 10√7 m)
Cevap:

UV = 10√7 m
Alanın doğal sayı olması için kısa kenar da √7 ile çarpılmış bir sayı olmalıdır.
Yani kısa kenar x = k√7 (k doğal sayı)

Örnekler:
k = 1 → x = √7 m
k = 2 → x = 2√7 m
k = 3 → x = 3√7 m

4. Öğrencilerin belirttiği ifadelerden hangisi, √800 ile çarpıldığında işlemin sonucu bir doğal sayı olur?
Cevap:

√800 ile çarpıldığında sonucu doğal sayı olan ifade bulunacak.

√800 = √(16×50) = 4√50 = 20√2

Her biriyle çarpalım:

Elif: √27 = 3√3 → 20√2 × 3√3 = 60√6 → irrasyonel

Zeynep: √32 = 4√2 → 20√2 × 4√2 = 80√4 = 160 → doğal sayı

Mert: √125 = 5√5 → 20√2 × 5√5 = 100√10 → irrasyonel

Sonuç: Zeynep’in belirttiği √32 ifadesi doğrudur.