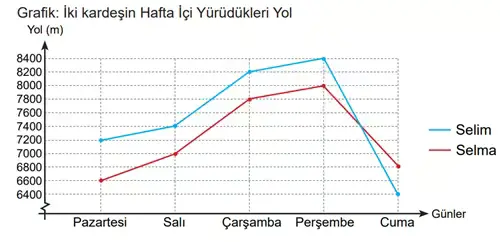
8. Sınıf Matematik Ders Kitabı Sayfa 89-90-91-92-93-94. Cevapları
8. Sınıf Matematik Ders Kitabı Sayfa 89-90-91-92-93-94. Cevapları MEB Yayınları bölümünde, ders kitabı sayfa 89-90-91-92-93-94 konularına ait cevapları bulabilirsiniz. “Gerçek Sayılar Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 89-90-91-92-93-94. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Gerçek Sayılar Cevapları
2. Ünite 1. Bölüm Kareköklü İfadeler: Devirli ondalık gösterimler rasyonel sayılardır çünkü iki tam sayının oranı olarak ifade edilebilirler. İrrasyonel sayılar ise ondalık gösterimleri sonsuz ve tekrarsız olan sayılardır.
İçindekiler
8. Sınıf Matematik Ders Kitabı Sayfa 89 Cevapları MEB Yayınları

Sizce devirli ondalık gösterimler irrasyonel sayı mıdır?
Cevap:
Hayır, devirli ondalık gösterimler irrasyonel sayı değildir.
Bunlar rasyonel sayılardır çünkü iki tam sayının birbirine bölümü şeklinde yazılabilirler.
Genel olarak bir sayı
x = 0,‾a₁a₂…aₖ (yani a₁a₂…aₖ kısmı sürekli tekrar ediyor)
şeklindeyse, bu sayı şu şekilde yazılabilir:
10ᵏx = a₁a₂…aₖ,‾a₁a₂…aₖ
Şimdi iki ifadeyi birbirinden çıkaralım:
10ᵏx – x = a₁a₂…aₖ
Buradan,
x = a₁a₂…aₖ / (10ᵏ – 1)
elde edilir. Bu ifade iki tam sayının oranıdır, dolayısıyla rasyonel sayıdır.
Örnek 1:
0,‾3 = 3 / 9 = 1 / 3
Örnek 2:
0,‾56 = 56 / 99
Sonuç:
Devirli ondalık sayılar rasyoneldir.
İrrasyonel sayılar ise ondalık kısmı sonlu olmayan ve hiçbir zaman tekrar etmeyen sayılardır.
Örneğin: π, √2, √3 gibi.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
8. Sınıf Matematik Ders Kitabı Sayfa 90 Cevapları MEB Yayınları
Sıra Sizde 1
Aşağıdaki sayıların irrasyonel sayı olup olmadıklarını belirleyiniz.
Cevap:
a) 6,3 → Ondalığı sonlu olduğu için rasyonel sayıdır.
b) 8,444… → Devirli ondalık olduğu için rasyonel sayıdır.
c) 0 → Tam sayı olduğu için rasyonel sayıdır.
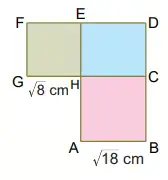
ç) √18 → Tam kare olmayan bir sayının karekökü olduğu için irrasyonel sayıdır.
d) −√16 → √16 = 4 olduğu için −√16 = −4’tür, bu nedenle rasyonel sayıdır.
e) −√0,04 → √0,04 = 0,2 olduğu için −0,2’dir, yani rasyonel sayıdır.
f) √0,9 → √0,9 = √(9/10) = 3√10 / 10 olur, √10 irrasyonel olduğu için sonuç irrasyonel sayıdır.
8. Sınıf Matematik Ders Kitabı Sayfa 91 Cevapları MEB Yayınları
Sıra Sizde 2
Aşağıdaki sayı ve ifadelerin hangi kümeye ait olduklarını örnekteki gibi işaretleyerek belirleyiniz
Cevap:
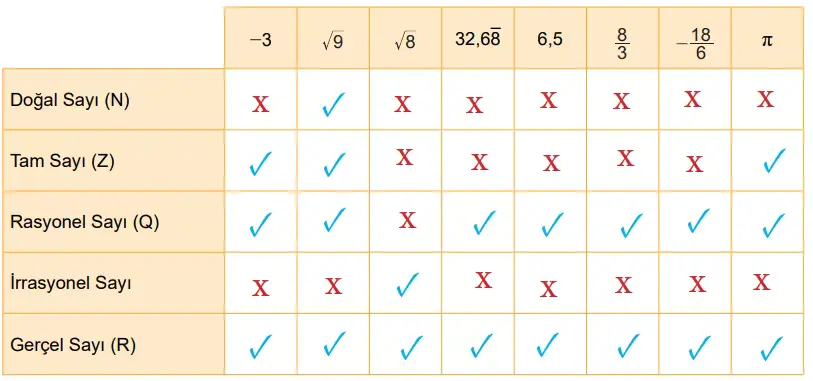
√9 = 3 → Doğal, tam ve rasyoneldir.
√8 ≈ 2,828… → Tekrarsız sonsuz ondalıktır, irrasyoneldir.
32,68̅ → Devirli ondalık, rasyoneldir.
6,5 → Kesir şeklinde (13/2) yazılabilir, rasyoneldir.
8/3 ve −18/6 → Kesir oldukları için rasyoneldir (−18/6 = −3 ayrıca tam sayıdır).
π → İrrasyoneldir.
Bütün bu sayılar gerçel sayıdır (R) kümesinde yer alır.
8. Sınıf Matematik Ders Kitabı Sayfa 92 Cevapları MEB Yayınları
Düşünme Zamanı
Üzerinde on iki gerçek sayının yazılı olduğu şeritlerle ilgili bilgiler aşağıda verilmiştir.
• Şeritlerde yazan harfler bulunduğu basamaklardaki rakamları temsil etmektedir.
• Şeritler üzerinde en fazla iki rasyonel sayı yan yana yerleştirilmiştir.
• Şeritler üzerinde en fazla iki irasyonel sayı yan yana yerleştirilmiştir.
Buna göre her şerit için harflerin alabileceği en büyük değerlerin toplamını bulunuz.
Cevap:
2m 38s boyunca düşündüm
a) En büyük değerler: A = 3, B = 8, C = 6.
A + B + C = 17
b) En büyük değerler: K = 9, L = 9, M = 4.
K + L + M = 22
c) En büyük değerler: X = 9, Y = 6, Z = 2.
X + Y + Z = 17
8. Sınıf Matematik Ders Kitabı Sayfa 93 Cevapları MEB Yayınları
Alıştırmalar Cevapları
1 Aşağıdaki ifadelerin eşit olduğu ondalık gösterimleri yazınız.
Cevap:
a) √0,81 = 0,9 çünkü 0,9 × 0,9 = 0,81
b) √1,44 = 1,2 çünkü 1,2 × 1,2 = 1,44
c) √0,0289 = 0,17 çünkü 0,17 × 0,17 = 0,0289
ç) √0,0196 = 0,14 çünkü 0,14 × 0,14 = 0,0196
Sonuç: 0,9 — 1,2 — 0,17 — 0,14
2. (5√0,16 + 15√0,36) / (8√0,25 + 2√2,25) işleminin sonucunu bulunuz.
Cevap:
Kökleri sadeleştirelim:
√0,16 = 0,4
√0,36 = 0,6
√0,25 = 0,5
√2,25 = 1,5
Yerlerine yazalım:
(5 × 0,4 + 15 × 0,6) / (8 × 0,5 + 2 × 1,5)
= (2 + 9) / (4 + 3)
= 11 / 7 ≈ 1,57
Sonuç: 11/7 veya yaklaşık 1,57
3. Alanı 0,0144 metrekare olan karenin bir kenar uzunluğunun, alanı 0,81 desimetrekare olan bir karenin bir kenar uzunluğundan kaç santimetre fazla olduğunu bulunuz.
Cevap:
İlk karenin alanı 0,0144 m² → kenarı √0,0144 = 0,12 m = 12 cm
İkinci karenin alanı 0,81 dm² → kenarı √0,81 = 0,9 dm = 9 cm
12 − 9 = 3 cm fark vardır.
Sonuç: 3 cm
4. √(4·10⁻⁴) + √(16·10⁻²) işleminin sonucunu bulunuz.
Cevap:
Her ifadeyi ayrı köke ayıralım:
√(4·10⁻⁴) = √4 × √10⁻⁴ = 2 × 10⁻² = 0,02
√(16·10⁻²) = √16 × √10⁻² = 4 × 10⁻¹ = 0,4
Toplayalım: 0,02 + 0,4 = 0,42
Sonuç: 0,42
5. Aşağıdaki ifadelerden doğru olanların başına “D”, yanlış olanların başına “Y” yazınız.
Cevap:
- Her tam sayı bir rasyonel sayıdır. → Doğru (örnek: −3 = −3/1)
- Her rasyonel sayı bir tam sayıdır. → Yanlış (örnek: 1/2 tam sayı değildir)
- Gerçek sayılar rasyonel ve tam sayılardan oluşur. → Yanlış (gerçek sayılar = rasyonel + irrasyonel)
- Bir doğal sayının karesi irrasyonel olabilir. → Yanlış (doğal sayıların kareleri her zaman rasyoneldir)
- Rasyonel ve irrasyonel sayıların ortak elemanı yoktur. → Doğru

8. Sınıf Matematik Ders Kitabı Sayfa 94 Cevapları MEB Yayınları
6. Aşağıdaki ifadelerin doğal sayıya eşit olabilmesi için değişkenlerin yerine yazılabilecek en küçük pozitif tam sayıları bulunuz.
Cevap:
a) √(8+x)
8+x bir tam kare olmalı. En küçük tam kare 9 olduğuna göre 8+x=9 ⇒ x=1.
b) √(24−y)
24-y bir tam kare olmalı. 24-y=16 (en yakın ve en küçük y>0 için) olduğunda y=8.
c) √(8·z)
8z bir tam kare olmalı. 8=2³ olduğundan en küçük z değeri 2 alınır (8·2=16), yani z=2.
ç) √(12/t)
12/t tam kare doğal sayı olmalı; bölenleri kontrol edince t=3 için 12/3=4 olur. En küçük pozitif t=3.
Sonuç: a) x=1, b) y=8, c) z=2, d) t=3.
7. √(24 + a) ve √(13 − a) ifadelerinin rasyonel sayı kümesinin elemanı olabilmesi için a değişkeninin yerine yazılabilecek pozitif tam sayıyı bulunuz.
Cevap:
Bir tam sayının karekökü rasyonel ise içi tam karedir. O hâlde hem 24+a hem de 13-a tam kare olmalı. Toplarsak
(24+a)+(13-a)=37=m²+n².
Karelerin toplamı 37 olan tek çift 36+1. Böylece 24+a=36 ve 13-a=1 verir; her ikisi de a=12 ile tutarlı.
Sonuç: a=12.
8. Yanda kareli zemine çizilmiş şeklin alanı 3,04 santimetrekaredir.
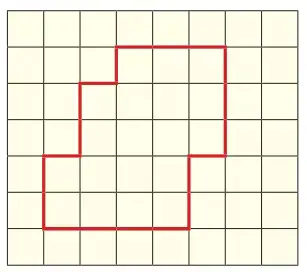
Buna göre bu şeklin çevre uzunluğunun kaç santimetre olduğunu bulunuz.
Cevap:
Görüntüden (kareli zemine bakarak) şekil 19 küçük kareyi kaplıyor (kare hücreleri sayılarak veya görüntü analizi ile). Verilen toplam alan 3,04 cm² olduğuna göre her küçük karenin alanı
3,04/19=0,16 cm²,
yani bir karenin kenarı √0,16=0,4 cm.
Şeklin hücresel (karel) çevresi —birim kenar sayısı olarak— 20’dir (her dolu hücrenin etrafındaki boş hücre kenarları sayılarak elde edilir). Buna göre gerçek çevre
20×0,4=8,0 cm.
Sonuç: 8 cm.
9. a pozitif bir tam sayı, √12 ifadesi ile √a ifadesinin çarpımı rasyonel sayıya eşit ve 3 < √a < 7’dir.
Buna göre bu şartları sağlayan a tam sayılarının toplamını bulunuz.
Cevap:
√12·√a=√(12a) rasyonel olabilmesi için 12a bir tam kare olmalı. Yazarsak 12a tam kare ise 3a de tam kare olur (çünkü 12 = 4·3, 4 zaten kare). Dolayısıyla a=3s² biçiminde olmalıdır.
Ayrıca 3<√a<7 ⇒ 9<a<49. Bu aralıkta a=3s² olan s değerleri için s²∈{4,9,16} (çünkü 3·4=12, 3·9=27, 3·16=48 ve bunlar 10–48 aralığında). Böylece uygun a değerleri: 12, 27, 48. Toplamları
12+27+48=87.
Sonuç: 87.