8. Sınıf Matematik Ders Kitabı Sayfa 92-95. Cevapları

8. Sınıf Matematik Ders Kitabı Sayfa 92-95. Cevapları Sonuç Yayınları bölümünde, ders kitabı sayfa 92-93-94-95 konularına ait cevapları bulabilirsiniz. “Gerçek Sayılar Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 8. Sınıf Matematik Ders Kitabı Sayfa 92-95. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.

Gerçek Sayılar Etkinlik Cevapları

2. Ünite Kareköklü İfadeler: Rasyonel sayılar kesir olarak ifade edilebilen sayılardır, irrasyonel sayılar ise ondalık gösterimi sonsuz ve tekrarsız olan sayılardır. Gerçel sayılar kümesi, hem rasyonel hem de irrasyonel sayıların tamamını içeren en geniş sayı kümesidir.

İçindekiler

8. Sınıf Matematik Ders Kitabı Sayfa 92 Cevapları Sonuç Yayınları

Kaan, projesi için kâğıda bir ABCD karesi ve karenin bir köşegenini çizdi. Çizdiği [BD] köşegenine bakan Kaan, ünlü matematikçi Pisagor’un “Kenar uzunluğu 1 birim olan bir karenin köşegen uzunluğu bir rasyonel sayı olarak ifade edilemez.” sözünü hatırladı. Kaan, rasyonel sayı olarak ifade edilemeyen bir sayının nasıl ifade edilebileceğini düşündü. Sizce rasyonel olan ve rasyonel olmayan sayıların tamamının bulunduğu bir küme olabilir mi? Nedenini açıklayınız.
Cevap: Evet, rasyonel olan ve rasyonel olmayan sayıların tamamının bulunduğu bir küme vardır. Bu küme gerçel sayılar kümesidir (ℝ).

Rasyonel sayılar (kesir şeklinde yazılabilen sayılar) ile irrasyonel sayılar (kesir şeklinde yazılamayan, ondalık kısmı düzensiz ve sonsuz olan sayılar) birlikte gerçel sayılar kümesini oluştururlar.

Yani:
Gerçel sayılar kümesi = Rasyonel sayılar ∪ İrrasyonel sayılar

Bu nedenle, hem rasyonel hem de irrasyonel tüm sayılar ℝ (gerçel sayılar kümesi) içinde bulunur.

Farklı bir sayfa mı arıyorsunuz?

İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:

MEB Yayınları SONUÇ Yayıncılık Tüm Kitaplar

8. Sınıf Matematik Ders Kitabı Sayfa 95 Cevapları Sonuç Yayınları

Alıştırmalar

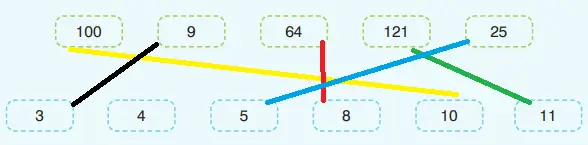
1. Aşağıdakilerden irrasyonel sayı olanların yanlarındaki kutucuklara ✓ işareti koyunuz.

a) 17,2133121593…
➡ Bu sayı ondalık olarak sonsuz ve tekrarsız devam ediyor.
➡ Sonsuz ve tekrarsız ondalık sayı irrasyoneldir.

b) 81,1̅8 (81,18888…)
➡ Virgülden sonra 8 rakamı sürekli tekrar ediyor.
➡ Tekrarlı ondalık sayılar rasyoneldir.

c) 7,36
➡ Virgülden sonra iki basamakta bitiyor.
➡ Sonlu ondalık sayılar rasyoneldir.

ç) π (pi sayısı)
➡ π sayısı sonsuz ve tekrarsız ondalık bir sayıdır.
➡ İki tam sayının oranı şeklinde yazılamaz. İrrasyoneldir.

d) 1286,222222…
➡ Virgülden sonra 2 rakamı sürekli tekrar ediyor.
➡ Tekrarlı ondalık sayılar rasyoneldir.

e) √1
➡ √1 = 1 olur.
➡ 1 bir tam sayı ve rasyoneldir.

f) √307
➡ 307 sayısı tam kare değildir.
➡ Tam kare olmayan sayıların karekökü irrasyoneldir.

g) √196
➡ 196 = 14² olduğundan √196 = 14 olur.
➡ 14 tam sayı olduğu için rasyoneldir.

Sonuç: İrrasyonel olanlar → a), ç), f)

2. Kareli alana üç adet rasyonel, dört adet irrasyonel sayı yazınız. Sayıları yazarken nelere dikkat ettiğinizi açıklayınız.
Cevap:

Rasyonel sayılar:
1/2 , -3 , 7,36

İrrasyonel sayılar:
π , √2 , √307 , 17,2133121593…

Rasyonel sayılar iki tam sayının oranı şeklinde yazılabilen, ondalık gösterimi sonlu veya tekrarlı olan sayılardır.
İrrasyonel sayılar ise ondalık gösterimi sonsuz ve tekrarsız olan, ayrıca tam kare olmayan sayıların karekökleriyle π gibi özel sayılardır.

3. Aşağıdaki işlemleri yapınız. İşlem sonuçlarının ait olduğu sayı kümelerini belirleyiniz.

3. a) 7·(√243 − √75) − 28√3 =

Adım 1: √243 = √(81·3) = 9√3
Adım 2: √75 = √(25·3) = 5√3
Adım 3: √243 − √75 = (9√3 − 5√3) = 4√3
Adım 4: 7·4√3 = 28√3
Adım 5: 28√3 − 28√3 = 0

Sonuç: 0
Kümeler:
0 ∈ N (doğal sayılar)
0 ∈ Z (tamsayılar)
0 ∈ Q (rasyonel sayılar)
0 ∈ R (gerçek sayılar)

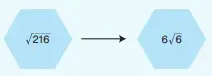
b) √2·(3√2 − √12) =

Adım 1: √2·3√2 = 3·2 = 6
Adım 2: √2·√12 = √24 = 2√6
Adım 3: 6 − 2√6

Sonuç: 6 − 2√6
Kümeler: İrrasyonel sayı (I), ayrıca gerçek sayı (R)