6. Sınıf Matematik Ders Kitabı Sayfa 120-121-122-123. Cevapları
6. Sınıf Matematik Ders Kitabı Sayfa 120-121-122-123. Cevapları 1. Kitap bölümünde, ders kitabı sayfa 120-121-122-123 konularına ait cevapları bulabilirsiniz. “3. Tema Hazır Mıyız? Etkinlik Cevapları” ve “3. Tema Başlayalım Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 6. Sınıf Matematik Ders Kitabı Sayfa 120-121-122-123. Cevapları MEB Yayınları soruları dikkatlice inceleyin. Başarınızı artırın.
3. Tema Hazır Mıyız? Cevapları
3. Tema: Sayılar ve Nicelikler (2): Ondalık kesirler ve doğal sayılarla yapılan işlemler, günlük hayatta ölçüm, paylaşım ve hesaplama gibi birçok durumda kullanılır. Çarpma ve bölme işlemleri birbirinin tersi olup, bu ilişki ondalık gösterimlerde de geçerlidir.
İçindekiler
6. Sınıf Matematik Ders Kitabı Sayfa 120 Cevapları Birinci Kitap
Hazır Mıyız?
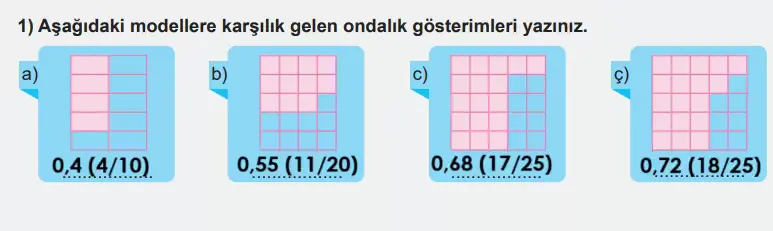
1) Aşağıdaki modellere karşılık gelen ondalık gösterimleri yazınız.
Cevap: Boyalı kısımları kesir olarak bulup ondalığa çevirdim.
a) 0,4 (4/10)
Ondalık olan: 0,4
Kesir olan: 4/10
b) 0,55 (11/20)
Ondalık olan: 0,55
Kesir olan: 11/20
c) 0,68 (17/25)
Ondalık olan: 0,68
Kesir olan: 17/25
ç) 0,72 (18/25)
Ondalık olan: 0,72
Kesir olan: 18/25
2) Aşağıdaki problemleri çözünüz. Bu problemlerin çözümünde kullandığınız sayı cümlelerini yazınız. Bulduğunuz sonuçların 1’den küçük veya büyük olma durumunu inceleyerek arkadaşlarınızla paylaşarak tartışınız.
a) Bir çiftlikteki 5 inekten günde toplam 7 litre süt alınmaktadır. Her bir inekten günde ortalama kaç litre süt alınmaktadır?
Cevap:
Sayı cümlesi:
7 ÷ 5 = 1,4
Her bir inekten 1,4 litre süt alınmaktadır.
Sonucun değerlendirmesi:
1,4 → 1’den büyük (çünkü 1 litreden biraz fazla süt alınıyor).
b) 42 kilogram cevizi 15 arkadaş eşit olarak paylaşmıştır. Her birine kaç kilogram ceviz düştüğünü hesaplayınız.
Cevap:
Sayı cümlesi:
42 ÷ 15 = 2,8
Her birine 2,8 kilogram ceviz düşer.
Sonucun değerlendirmesi:
2,8 → 1’den büyük (her kişiye 1 kilodan fazla düşüyor).
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
6. Sınıf Matematik Ders Kitabı Sayfa 121 Cevapları Birinci Kitap
3) Paydaları eşit iki kesrin toplanıp çıkarılmasını gerektiren bir problem kurunuz. Kurduğunuz problemin çözümünde matematiksel temsilleri (sayı doğrusu veya modelleme) kullanınız. Paydaları eşit kesirlerde toplama veya çıkarma işlemlerinin nasıl yapıldığını açıklayınız.
Cevap:
Problem
Ayşe sabah portakal suyunun 3/8’ini içti.
Öğle vakti aynı şişeden 2/8 daha içti.
Ayşe toplamda portakal suyunun ne kadarını içmiştir?
Çözüm
3/8 + 2/8 = 5/8
Açıklama
Paydaları eşit olan kesirlerde toplama veya çıkarma işlemi yapılırken:
Paylar toplanır veya çıkarılır.
Payda aynı kalır.
Örneğin:
3/8 + 2/8 = 5/8
Paydalar aynıysa paylar toplanır, payda değişmez.
5/8 − 2/8 = 3/8
Paydalar aynıysa paylar çıkarılır, payda yine değişmez.
Sonuç: Ayşe portakal suyunun 5/8’ini içmiştir.
4) Aşağıdaki problemleri çözünüz. Çözümlerinizi arkadaşlarınızla paylaşarak tartışınız.
a) Bir çiftlikte 120 tavuk bulunmaktadır. Bu tavukların 3/8’ü beyaz, geri kalanı kahverengidir. Çiftlikte kaç beyaz ve kaç kahverengi tavuk vardır?
Cevap:
Bir çiftlikte 120 tavuk vardır.
Tavukların 3/8’i beyaz, geri kalanı kahverengidir.
Beyaz tavuk sayısı:
120 × 3/8 = (120 ÷ 8) × 3 = 15 × 3 = 45
Kahverengi tavuk sayısı:
120 − 45 = 75
Sonuç: 45 beyaz tavuk, 75 kahverengi tavuk vardır.
b) Bir sınıftaki öğrencilerin 3/8’ü kız, geri kalanı erkektir. Sınıfta 12 kız öğrenci olduğuna göre erkek öğrenci sayısını bulunuz.
Cevap:
Bir sınıfta öğrencilerin 3/8’i kız.
Sınıfta 12 kız öğrenci olduğuna göre toplam öğrenci sayısını bulalım:
Toplam öğrenci sayısı:
12 ÷ (3/8) = 12 × (8/3) = 32
Erkek öğrenci sayısı:
32 − 12 = 20
Sonuç: 12 kız, 20 erkek öğrenci vardır.
5) Doğal sayılarla çarpma ve bölme işlemlerinin anlamlarını ve arasındaki ilişkileri açıklayınız. Sizce bu ilişki ondalık gösterimlerde çarpma ve bölme işlemlerinde de geçerli olabilir mi? Fikirlerinizi arkadaşlarınızla paylaşarak tartışınız.
Cevap:
Doğal sayılarda çarpma işlemi, bir sayının kendisi kadar tekrar toplanması anlamına gelir.
Örneğin: 4 × 3 = 12 işlemi, 4 + 4 + 4 = 12 anlamındadır.
Bölme işlemi ise bir sayının eşit parçalara ayrılması ya da bir sayının içinde diğer sayının kaç kez olduğunu bulma işlemidir.
Örneğin: 12 ÷ 3 = 4 işlemi, 12 sayısının 3’erli gruplara ayrıldığında her grupta 4 olduğunu gösterir.
Çarpma ve bölme birbirinin tersi işlemleridir.
Çünkü 4 × 3 = 12 ise, 12 ÷ 3 = 4 olur.
Bu ilişki ondalık sayılarda da geçerlidir.
Örneğin: 0,4 × 10 = 4 ve 4 ÷ 10 = 0,4 olur.
Yani çarpma büyütürken, bölme küçültür.
6. Sınıf Matematik Ders Kitabı Sayfa 122 Cevapları Birinci Kitap
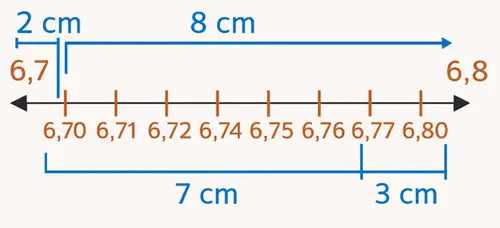
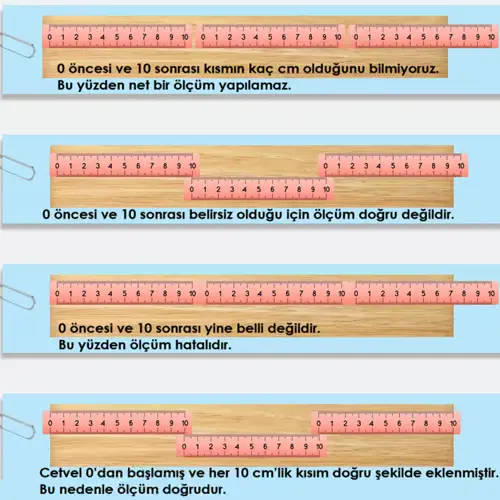
6) Aşağıda bir tahta parçasının uzunluğu dört farklı şekilde ölçülmüştür. Bu ölçümleri inceleyerek bunlardan hangilerinin doğru olabileceği hakkındaki düşüncelerinizi altlarına yazınız. Fikirlerinizi arkadaşlarınızla paylaşarak tartışınız.
Cevap:
1. Ölçüm:
0 öncesi ve 10 sonrası kısmın kaç cm olduğunu bilmiyoruz.
Bu yüzden net bir ölçüm yapılamaz.
2. Ölçüm:
0 öncesi ve 10 sonrası belirsiz olduğu için ölçüm doğru değildir.
3. Ölçüm:
0 öncesi ve 10 sonrası yine belli değildir.
Bu yüzden ölçüm hatalıdır.
4. Ölçüm:
Cetvel 0’dan başlamış ve her 10 cm’lik kısım doğru şekilde eklenmiştir.
Bu nedenle ölçüm doğrudur.
3. Tema Başlayalım Cevapları
6. Sınıf Matematik Ders Kitabı Sayfa 123 Cevapları Birinci Kitap
Başlayalım
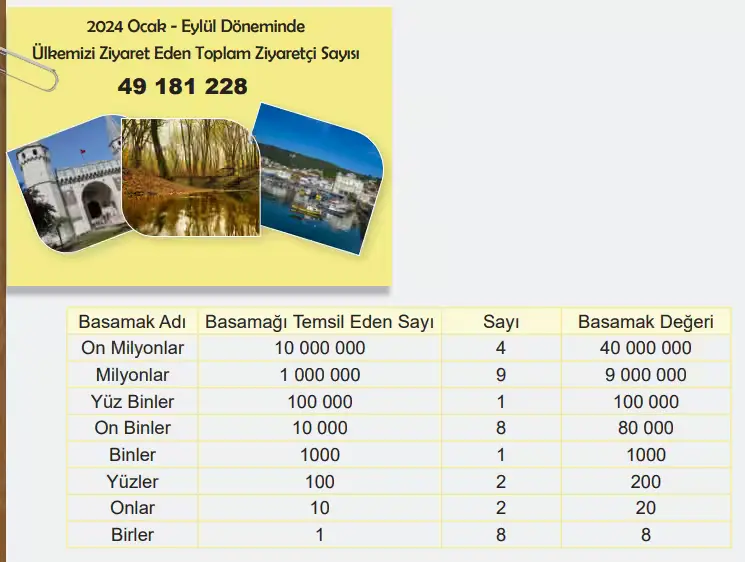
Yandaki görselde 2024 yılı Ocak-Eylül döneminde ülkemizi ziyaret eden toplam ziyaretçi sayısı verilmiştir.
Verilen dönemde ülkemize gelen toplam turist sayısının basamak tablosu aşağıda gösterilmiştir
Buna göre aşağıdaki soruları cevaplayınız.
a) Basamağı temsil eden sayıların oluşturduğu azalan örüntünün her bir adımında bulunan sayıyı sırasıyla yazınız.
Cevap:
40.000.000 → 49.000.000 → 49.100.000 → 49.180.000 → 49.181.000 → 49.181.200 → 49.181.220 → 49.181.228
Bu örüntüde her adımda, bir sonraki basamağın değeri eklenerek sayı tamamlanmıştır.
Yani en soldaki basamaktan başlanarak tüm basamak değerleri sırayla toplanmıştır.
b) Yazdığınız örüntünün ilk adımından önce bir adım daha olsaydı bu adıma hangi sayı yazılırdı? Fikirlerinizi yazarak arkadaşlarınızla tartışınız.
Cevap: İlk adımdan önce bir adım daha olsaydı, sayı 10 kat artardı.
Bu durumda 10 000 000 × 10 = 100 000 000 (yüz milyon) olurdu.
Yani örüntü sola doğru ilerlediğinde sayı her adımda 10 kat büyür.
c) Yazdığınız örüntü bir adım daha devam ettirilirse bu adımda hangi sayı bulunur? Fikirlerinizi yazarak arkadaşlarınızla tartışınız.
Cevap: Örüntü bir adım daha devam ettirilirse, son sayı 1’in 10’a bölünmesiyle oluşur.
Bu durumda basamağı temsil eden sayı 0,1 (bir onda bir) olur.
Yani örüntü sağa doğru ilerlediğinde sayı 10’a bölünerek küçülür.