6. Sınıf Matematik Ders Kitabı Sayfa 124-125-126-127. Cevapları
6. Sınıf Matematik Ders Kitabı Sayfa 124-125-126-127. Cevapları 1. Kitap bölümünde, ders kitabı sayfa 124-125-126-127 konularına ait cevapları bulabilirsiniz. “Ondalık Gösterimlerde Basamak Değeri Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 6. Sınıf Matematik Ders Kitabı Sayfa 124-125-126-127. Cevapları MEB Yayınları soruları dikkatlice inceleyin. Başarınızı artırın.
Ondalık Gösterimlerde Basamak Değeri Cevapları
3. Tema: Sayılar ve Nicelikler (2): Ondalık gösterimler, kesirlerin daha kolay yazılıp okunmasını sağlayan bir sistemdir. Virgülden sonraki basamaklar sırasıyla onda birler, yüzde birler ve binde birleri ifade eder.
İçindekiler
6. Sınıf Matematik Ders Kitabı Sayfa 124 Cevapları Birinci Kitap
Etkinlik 1: Tarihte Ondalık Gösterim
Sınıfınızda üç grup oluşturunuz. Grup arkadaşlarınızla yukarıdaki bilgileri inceleyiniz. Daha sonra grup olarak bir bilim insanını seçerek aşağıdaki soruları cevaplayınız.
a) Seçtiğiniz bilim insanıyla ilgili verilen bilgileri göz önünde bulundurarak ondalık gösterimlerin kesir ile ilişkisinin nasıl kurulabileceğini ve basamak değerlerinin nasıl ifade edilebileceğini grup arkadaşlarınızla tartışınız.
Cevap:
Grup: Stevin (Sitivin):
- Stevin, ondalık kesirlerin yazılışını standartlaştırdığı için sayı basamakları şu şekilde gösterilir:
- Ondalık sayılarda virgülden sonraki ilk basamak onda birleri (0,1)
- İkinci basamak yüzde birleri (0,01)
- Üçüncü basamak binde birleri (0,001) gösterir.
- Örnek olarak: 0,234 sayısı:
2: onda birler
3: yüzde birler
4: binde birler
b) Ulaştığınız sonuçları diğer gruplarla paylaşınız. Diğer grupların size soru sormasına izin verip, soruları dikkatli bir şekilde dinleyerek cevaplayınız. Grupların verdiği bilgilerden geçersiz olduğunu düşündüklerinizi açıklayınız.
Cevap: Kepler grubu kesirlerin bölme işlemiyle değil doğrudan ondalık olarak yazılmasının hesaplamaları kolaylaştırdığını savunarak karşı cevap bekleyecek olursa cevabımız, Stevin’in bu yazımı ilk kez sistemli hâle getirdiğini ve bu sayede bugünkü ondalık sistemin temellerinin atıldığını açıklarız.
c) Kâşî’nin ondalık gösterimlerle ilgili çalışmalarını araştırınız. Araştırmalarınızın sonucunda elde ettiğiniz bilgileri ve bu bilim insanının kültürel mirasımıza katkılarını arkadaşlarınızla paylaşarak tartışınız.
Cevap: Kaşi 15. yüzyılda yaşamış olan Türk matematikçi Ali Kuşçu’nun öğrencisidir. Ondalık kesirleri açıkça kullanan ilk bilim insanları arasındadır. π (pi) sayısını 16 basamağa kadar hesaplamıştır. Miftah el-Hisab eserinde kesirleri ondalık biçimde yazarak bu konuda öncülük etmiştir.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
6. Sınıf Matematik Ders Kitabı Sayfa 125 Cevapları Birinci Kitap
Etkinlik 2: Ondalık Gösterimi Kesirlerin Toplamı Şeklinde Yazma
Derya, kare şeklindeki 100 metrekarelik bahçesini birer metrekarelik kare şeklindeki bölmelere ayırmıştır.
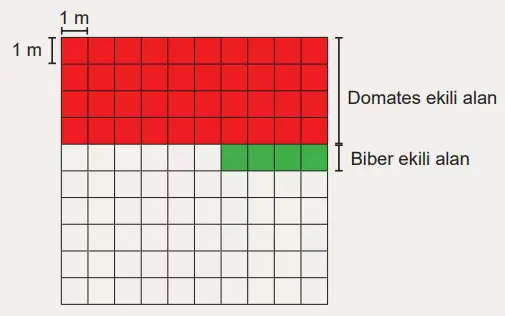
Bahçesinin 2/5’lik kısmına domates, 1/25’lik kısmına ise biber ekmiştir.
Verilenlere göre aşağıdaki soruları cevaplayınız.
a) Biber ekili alanın temsil ettiği kesir gösterimini paydası 100 olacak şekilde yazınız.
Cevap: Biber ekili alanın paydası 100 olacak şekilde yazalım:
1/25 = (1×4)/(25×4) = 4/100
Çünkü 25’i 100 yapmak için pay ve paydayı 4 ile çarptık.
Yani biber ekili alan bahçenin %4’ü kadardır.
b) Domates ekili alanın temsil ettiği kesir gösterimini paydası 10 olacak şekilde yazınız.
Cevap: Domates ekili alanın paydası 10 olacak şekilde yazalım:
2/5 = (2×2)/(5×2) = 4/10
Çünkü 5’i 10 yapmak için pay ve paydayı 2 ile çarptık.
Yani domates ekili alan bahçenin %40’ı kadardır.
c) Domates ve biber ekili alanın tamamının temsil ettiği ondalık gösterimi yazınız.
Cevap:
Domates ve biber ekili alanların toplamını bulalım:
2/5 + 1/25 = 10/25 + 1/25 = 11/25
11/25 = (11×4)/(25×4) = 44/100 = 0,44
Yani domates ve biber ekili alanlar birlikte bahçenin %44’ünü (0,44’ünü) kaplar.
ç) Toplam ekili alanın temsil ettiği ondalık gösterim ile domates ve biber ekili alanların ayrı ayrı temsil ettiği kesirlerin toplamı birbirine eşit olur mu? Bu kesirlerin ondalık gösterimin ondalık kısmındaki basamaklar olduğu söylenebilir mi? Fikirlerinizi arkadaşlarınızla paylaşarak tartışınız.
Cevap: Toplam ekili alanın ondalık gösterimi ile domates ve biber alanlarının ayrı ayrı ondalık gösterimlerinin toplamı eşittir.
Çünkü domates = 0,4 ve biber = 0,04’tür.
0,4 + 0,04 = 0,44 eder.
Bu da toplam alanın ondalık gösterimiyle aynıdır.
Sonuç: Kesirleri toplayıp ondalığa çevirmekle, ondalık sayıları toplayarak sonuca ulaşmak aynı sonucu verir.
6. Sınıf Matematik Ders Kitabı Sayfa 126 Cevapları Birinci Kitap
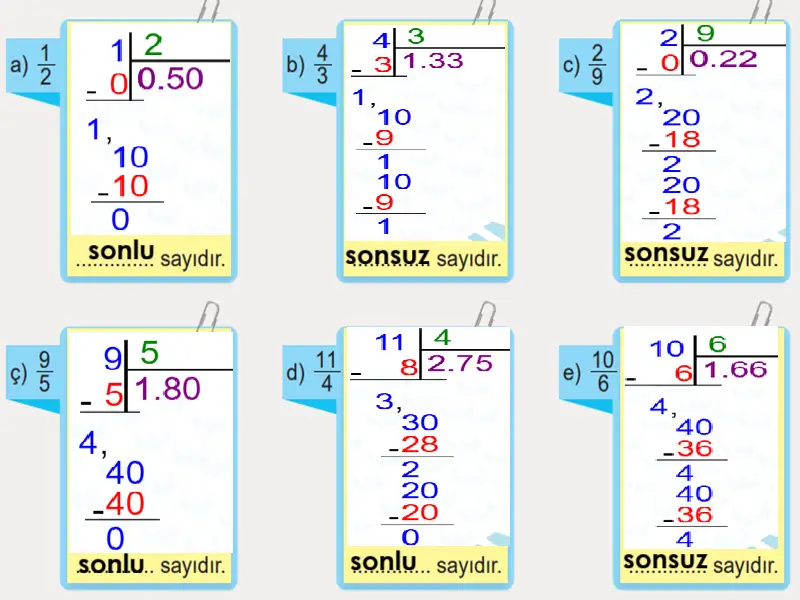
Örnek 1
Aşağıdaki kesir modellerine karşılık gelen ondalık gösterimleri bularak paydası 10, 100, 1000 olan kesirlerin toplamları biçiminde ifade ediniz.
Cevap:
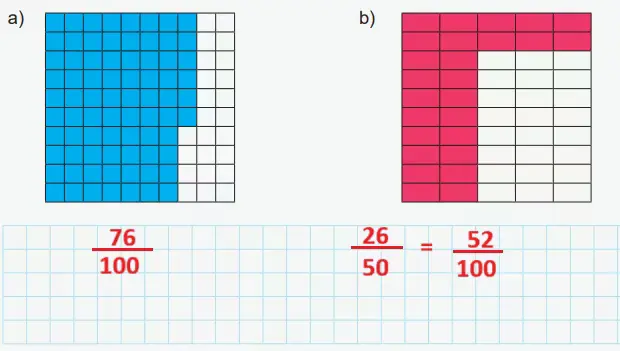
a)
Kesir: 76/100
Ondalık gösterim: 0,76
Kesirlerin toplamı biçiminde: 7/10 + 6/100
b)
Kesir: 26/50 = 52/100
Ondalık gösterim: 0,52
Kesirlerin toplamı biçiminde: 5/10 + 2/100
6. Sınıf Matematik Ders Kitabı Sayfa 127 Cevapları Birinci Kitap
Örnek 2
Aşağıdaki boş sayı doğrularının altında verilen yönergeleri uygulayınız. Daha sonra ikinci adımda belirlediğiniz ondalık gösterimi paydası 10, 100 veya 1000 olan kesirlerin toplamı biçiminde yazınız.
Cevap:
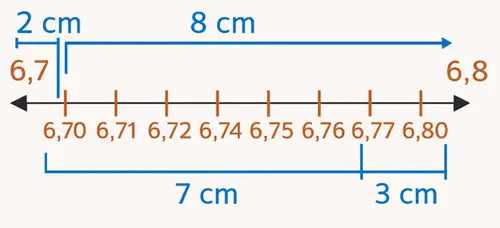
a)
3,8 ile 3,9 arasındaki fark 0,1’dir.
Her 1 cm = 0,01 olur.
3,8’in 3 cm sağındaki sayı = 3,83’tür.
Kesir biçimi: 3 + 83/100 → 3 + 8/10 + 3/100
b)
0,6 ile 0,7 arasındaki fark 0,1’dir.
Her 1 cm = 0,01 olur.
0,7’nin 4 cm solundaki sayı = 0,66’dır.
Kesir biçimi: 66/100 → 6/10 + 6/100
c)
1,81 ile 1,82 arasındaki fark 0,01’dir.
Her 1 cm = 0,001 olur.
1,81’in 1 cm sağındaki sayı = 1,811’dir.
Kesir biçimi: 1 + 811/1000 → 1 + 8/10 + 1/100 + 1/1000