7. Sınıf Matematik Ders Kitabı Sayfa 129-135. Cevapları MEB Yayınları

7. Sınıf Matematik Ders Kitabı Sayfa 129-135. Cevapları MEB Yayınları bölümünde, ders kitabı sayfa 129-130-131-132-133-134-135 konularına ait cevapları bulabilirsiniz. “Doğru Orantı – Ters Orantı Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 7. Sınıf Matematik Ders Kitabı Sayfa 129-135. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.

Doğru Orantı – Ters Orantı Cevapları

4. ÜNİTE Veri Analizi ve Yüzdeler: 7. Sınıf Matematik Ders Kitabı Sayfa 129-130-131-132-133-134-135. Cevapları MEB Yayınları

7. Sınıf Matematik Ders Kitabı Sayfa 129 Cevapları MEB Yayınları

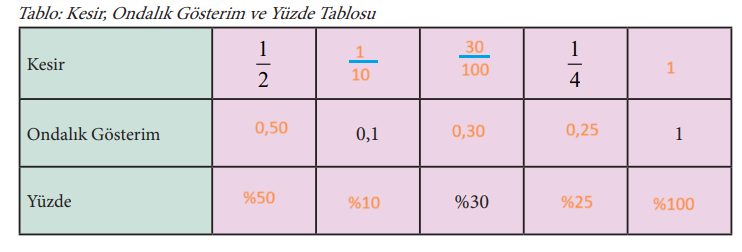
➢ Kullanılması gereken buğday miktarı fındık miktarının kaç katıdır?
Cevap:  3/1 ÷ 1/2 = 3/1 . 2/1 = 6 katıdır.

➢ 1 bardak buğdaya düşen şeker miktarını hesaplayınız.
Cevap:

Şeker → 4
Buğday → 3
1 bardak buğdaya düşen şeker miktarı → 4/3

➢ Tabloya göre 2 bardak üzüm kullanılarak kaç bardaklık aşure malzemesi oluşturulabilir?
Cevap: Yarım su bardağı üzüm ile 1 aşure yapılıyorsa 2 bardak üzüm ile 4 aşure yapılır.

0,5       1
2          x
2 = 0,5x
4 = x

➢ Bir bardak, yaklaşık 200 gr malzeme almaktadır. Tabloya göre 3 bardak fındık kullanılarak kaç gramlık aşure malzemesi oluşturulabilir
Cevap: Yarım su bardağı ile bir aşure yapılıyorsa, 3 bardak fındıkla
3 bardak      x
0,5 bardak   1
0,5x = 3
x = 6

➢ 8 kişi için hazırlanmış olan aşure 10 kişiye dağıtılırsa kişi başına düşen aşure miktarı nasıl değişir?
Cevap:  10/8 = 5/4 olur

7. Sınıf Matematik Ders Kitabı Sayfa 135 Cevapları MEB Yayınları

SIRA SİZDE

1. a ve b doğru orantılı iki tam sayıdır. a = 8 olduğunda b = 5 olduğuna göre a = 24 olduğunda b kaç olur?
Cevap:

a/b = 8/5
8/5 = 24/b
8b = 24 . 5
8b = 120
b = 15 olur

2. Yandaki dikdörtgenin kenar uzunlukları 3 ve 4 ile doğru orantılıdır. Dikdörtgenin çevre uzunluğu 70 cm olduğuna göre kısa kenar uzunluğu kaç santimetredir?
Cevap:

Kısa kenar 3k
Uzun kenar 4k

Çevresi → 4k + 4k + 3k + 3k = 14k
14k = 70 cm
k = 5cm

Kısa kenar → 3k ise
3 . 5 = 15 cm’dir.

3. a/b = 2/3 ve a + b = 40 ise b rasyonel sayısı kaçtır?
Cevap:

a/b = 2/3 ise
a = 2k
b = 3k

2k + 3k = 40
5k = 40
k = 8

b = 3k → 3 . 8 = 24

4. Sabit hızla giden bir araba 2 saatte 90 km yol alabiliyorsa 3 saatte kaç km yol alır?
Cevap:

2 saat      90km
3 saat       x km
90 . 3 = 2xkm
270 = 2xkm
135 = x

5. Ölçeği 1 : 1 500 000 olan bir haritada iki şehir arası 9 cm olarak gösterilmiştir. Buna göre bu iki şehir arasındaki gerçek uzaklık kaç kilometredir?
Cevap:

1 500 000 x 9 = 13 500 000 cm
13 500 000 ÷ 100 000 = 135 km

6. Eşit kapasitede çalışan işçilerden sekizi bir işi 9 günde bitirmektedir. Bu işçilere 4 kişi daha katılırsa aynı işi kaç günde bitirirler?
Cevap:

8 işçi       9 gün
12 işçi      x gün
12 . 9 = 8x
108  = 8x
13,5 = x

7. Birbirine bağlı olarak dönen saat dişlilerinden küçük olan dişli 25 tam tur attığında büyük dişli 9 tam tur atmaktadır. Büyük dişlide 50 diş varsa küçük dişlinin diş sayısı kaçtır?
Cevap:

50 ÷ 25 = 2
2 . 9 = 18 diş vardır

8. Elif, okulunun bahçesinde bulunan 12 m uzunluğundaki bayrak direğinin gölgesini 3 m olarak ölçmüştür. Buna göre 180 cm boyundaki Elif ’in aynı andaki gölgesi kaç santimetredir?
Cevap:

1m = 100 cm

1200 direk      300 gölge
180 boy            x gölge
1200 x = 54000
x = 45 cm

9. (3x – 3) ile (y + 4) rasyonel sayıları ters orantılıdır. x = 5 olduğunda y = 5 oluyorsa y = 2 olduğunda x kaç olur?
Cevap:

(3x -3) . (y + 4) = k     (15 – 3) . (5 + 4) = 12 . 9 = 108 → k = 108
(3x -3) . (y + 4) = k     (3x – 3) . (5 + 4) = (3x – 3) . 9 = 108 → (3x – 3) = 12 → 3x = 15 → x = 5 olur

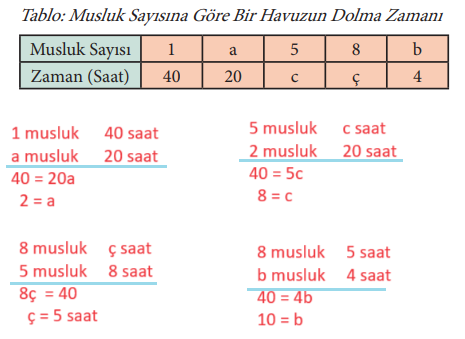
10. Aşağıdaki tabloda boş bir havuzu dolduran musluk sayısı ile havuzun dolma zamanı arasındaki ilişki verildiğine göre tablodaki harflerle ifade edilen yerlere gelmesi gereken sayıları bulunuz.
Cevap: