4. Sınıf Matematik Ders Kitabı Sayfa 122-124. Cevapları
4. Sınıf Matematik Ders Kitabı Sayfa 122-124. Cevapları Fersa Yayınları bölümünde, ders kitabı sayfa 122-123-124 konularına ait cevapları bulabilirsiniz. “Matematiksel İfadelerde Eşitliği Sağlama Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 4. Sınıf Matematik Ders Kitabı Sayfa 122-124. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.
Matematiksel İfadelerde Eşitliği Sağlama Cevapları
3. Ünite: Eşitliğin sağlanması için iki tarafın arasındaki fark bulunur ve küçük olan taraf bu fark kadar artırılır. Bu yöntemle matematiksel denklemlerde denge sağlanır.
İçindekiler
4. Sınıf Matematik Ders Kitabı Sayfa 122. Cevapları Fersa Yayıncılık
Hatırlayalım
Hangi sayının 2 katı, 20’nin yarısıdır? Söyleyiniz.
Cevap:
20’nin yarısını bulalım:
20 ÷ 2 = 10
20’nin yarısı 10 eder.
Hangi sayıyı 2 ile çarparsak 10 eder?
Çünkü 2 katı demek 2 ile çarpmak demektir.
2 × ? = 10
2 × 5 = 10
Sonuç: O zaman aradığımız sayı 5’tir.

Yeşilay Cemiyeti yurdumuzda tütün, alkol ve madde bağımlılığı gibi gençliğe ve topluma zarar veren alışkanlıklarla mücadele eder. Yeşilay Cemiyetine destek olmak isteyen Nezahat Onbaşı İlkokulu 4. sınıf öğrencileri, rozetler tasarladılar.
4/A sınıfındaki 16 öğrenciden her biri 6 rozet tasarladı. 4/B sınıfı öğrencileri 90 rozet tasarladılar. İki sınıfta tasarlanan rozet sayılarının eşit olması için 4/B sınıfı öğrencilerinin kaç tane daha rozet tasarlamaları gerektiği nasıl bulunabilir? Tartışınız.
Cevap:
4/A sınıfında 16 öğrenci vardır ve her biri 6 rozet tasarlamıştır.
Bu yüzden 4/A sınıfının yaptığı rozet sayısı:
16 × 6 = 96 rozet
4/B sınıfı ise 90 rozet tasarlamıştır.
İki sınıfın yaptığı rozet sayılarının eşit olması için, 4/B sınıfının 4/A sınıfı kadar rozet yapması gerekir.
Bu yüzden 4/A’nın toplamı olan 96’dan, 4/B’nin yaptığı 90 çıkarılır:
96 − 90 = 6
Sonuç: 4/B sınıfının 6 rozet daha tasarlaması gerekir.
Yapalım Öğrenelim
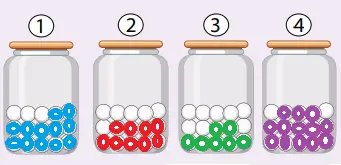
Boyanan misket sayıları:
- 1. kavanoz: 12
- 2. kavanoz: 9
- 3. kavanoz: 7
- 4. kavanoz: 13
1) İki kavanozu seçip toplamlarını yazalım.
Örnek olarak şöyle seçelim:
1. kavanoz + 2. kavanoz:
12 + 9
2) Eşit değil (≠) işaretini yazalım:
12 + 9 ≠
3) Diğer iki kavanozun toplamını sağ tarafa yazalım:
3. kavanoz + 4. kavanoz:
7 + 13
12 + 9 ≠ 7 + 13
4) İşlemleri yapalım:
- 12 + 9 = 21
- 7 + 13 = 20
21 ≠ 20
İşlemlerin sonuçları eşit değildir.
5) Eşitliğin sağlanması için neler yapılabilir?
- 1. grup toplamından 1 misket çıkarılabilir.
- 2. grup toplamına 1 misket eklenebilir.
- Ya da başka kavanozlar seçilerek eşit toplamlar oluşturulabilir.
Tartışma:
“İki tarafın toplamı farklı olduğu için eşit değildir. Eşitliğin sağlanması için bir taraftan misket azaltılabilir ya da diğer tarafa misket eklenebilir.”
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
4. Sınıf Matematik Ders Kitabı Sayfa 124. Cevapları Fersa Yayıncılık
Sen Olsan Ne Yapardın
Yukarıda verilen ifadede eşitliğin sağlanması için siz nasıl bir yöntem izlersiniz? Açıklayınız.
Cevap:
1) Önce iki tarafın sonuçlarına bakarım.
Örnekte:
- 84 ÷ 4 = 21
- 17 + 3 = 20
Bu iki sonuç eşit değil.
2) Eşitlemek için ne yapmalıyım diye düşünürüm.
21 ile 20 arasında 1 fark vardır.
3) Küçük olan tarafa gereken sayıyı eklerim.
20 daha küçük olduğu için:
20 + 1 = 21 olur.
Böylece iki taraf eşit olur.
Alıştırma Yapalım
Aşağıda verilen ifadelerde eşitliğin sağlanabilmesi için yapılması gereken işlemleri defterinizde yazarak gösteriniz.
Cevap:
Yöntem:
Önce sol tarafı hesaplıyoruz, sonra sağ tarafı hesaplıyoruz.
Sonuçlar eşit değilse, farkı küçük olana ekleyerek eşitliği sağlıyoruz.
1) 50 − 35 ≠ 7 × 4
50 − 35 = 15
7 × 4 = 28
Fark: 28 − 15 = 13
➡ 15’i 28 yapmak için 13 eklenir:
50 − 35 + 13 = 7 × 4
2) 6 × 8 ≠ 9 × 5
6 × 8 = 48
9 × 5 = 45
Fark: 48 − 45 = 3
➡ 45’i 48 yapmak için 3 eklenir:
6 × 8 = 9 × 5 + 3
3) 450 ÷ 50 ≠ 36 ÷ 2
450 ÷ 50 = 9
36 ÷ 2 = 18
Fark: 18 − 9 = 9
➡ 9’u 18 yapmak için 9 eklenir:
450 ÷ 50 + 9 = 36 ÷ 2
4) 134 + 12 ≠ 200 − 34
134 + 12 = 146
200 − 34 = 166
Fark: 166 − 146 = 20
➡ 146’yı 166 yapmak için 20 eklenir:
134 + 12 + 20 = 200 − 34
5) 64 − 5 ≠ 11 × 4
64 − 5 = 59
11 × 4 = 44
Fark: 59 − 44 = 15
➡ 44’e 15 eklenir:
64 − 5 = 11 × 4 + 15
6) 6 + 12 ≠ 24 − 4
6 + 12 = 18
24 − 4 = 20
Fark: 20 − 18 = 2
➡ 18’e 2 eklenir:
6 + 12 + 2 = 24 − 4
7) 16 + 18 ≠ 50 − 8
16 + 18 = 34
50 − 8 = 42
Fark: 42 − 34 = 8
➡ 34’e 8 eklenir:
16 + 18 + 8 = 50 − 8
8) 12 × 14 ≠ 50 + 42
12 × 14 = 168
50 + 42 = 92
Fark: 168 − 92 = 76
➡ 92’ye 76 eklenir:
12 × 14 = 50 + 42 + 76
9) 100 − 32 ≠ 5 × 11
100 − 32 = 68
5 × 11 = 55
Fark: 68 − 55 = 13
➡ 55’e 13 eklenir:
100 − 32 = 5 × 11 + 13
10) 24 + 65 ≠ 42 + 18
24 + 65 = 89
42 + 18 = 60
Fark: 89 − 60 = 29
➡ 60’a 29 eklenir:
24 + 65 = 42 + 18 + 29
11) 101 − 37 ≠ 82 − 19
101 − 37 = 64
82 − 19 = 63
Fark: 64 − 63 = 1
➡ 63’e 1 eklenir:
101 − 37 = 82 − 19 + 1
12) 182 ÷ 13 ≠ 196 ÷ 14
182 ÷ 13 = 14
196 ÷ 14 = 14
➡ Zaten eşit.
Her iki taraf da 14 olduğu için işlem yapılmasına gerek yoktur.