4. Sınıf Matematik Ders Kitabı Sayfa 125-126-127-128. Cevapları

4. Sınıf Matematik Ders Kitabı Sayfa 125-126-127-128. Cevapları Fersa Yayınları bölümünde, ders kitabı sayfa 125-126-127-128 konularına ait cevapları bulabilirsiniz. “3. Ünite Değerlendirme Çalışmaları Etkinlik Cevapları” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 4. Sınıf Matematik Ders Kitabı Sayfa 125-126-127-128. Cevapları soruları dikkatlice inceleyin. Başarınızı artırın.

3. Ünite Değerlendirme Çalışmaları Cevapları

3. Ünite: Çarpma ve bölme işlemlerinde sayıların özelliklerini kullanarak pratik hesaplamalar yapabiliriz. İşlemleri basitleştirmek için sayıları en yakın onluk veya yüzlüğe yuvarlayarak tahminler oluşturabiliriz.

4. Sınıf Matematik Ders Kitabı Sayfa 125. Cevapları Fersa Yayıncılık

Aşağıda verilen cümlelerde noktalı yerlere, verilen ifadelerden uygun olanları yazınız.
Cevap:

1. 125 x 16 işleminin sonucunun onlar basamağında 0 rakamı vardır.
2. 214 x 23 işleminin sonucunun rakamları toplamı 17 dir.
3. Çarpma işleminde çarpılan sayılara çarpan denir.
4. 120 x 48 işleminde çarpım 5 binlik, 7 yüzlük, 6 onluk, 0 birlikten oluşur.
5. İki basamaklı en küçük tek doğal sayı ile 100’ün çarpımı 1100 dir.

B. Aşağıda verilen ifadelerden doğru olanların başına “D”, yanlış olanların başına “Y” harfini yazınız.
Cevap:

1. (Y) 84 x 50 işleminin sonucunun rakamlarının toplamı 7’dir.
2. (D) 76 x 5 işleminin sonucunun rakamlarının toplamı 11’dir.
3. (D) 72 x 25 işleminin sonucunun rakamlarının toplamı 9’dur.
4. (D) 68 x 50 işleminin sonucu 3400’dür.
5. (Y) 42 x 5 işleminin sonucu 205’dir.
6. (D) 34 x 25 işleminin sonucu 850’dir

C. Aşağıdaki soruları yanıtlayınız.

1. (19 x 69 x 39) = 69 x (39 x ?)
Yukarıda verilen eşitlikte “?” yerine hangi sayı yazılmalıdır?
Cevap:

(19 × 69 × 39) = 69 × (39 × ?)

Her iki tarafta da 69 ve 39 var. Eksik olan sayı 19’dur.

Sonuç : 19

4. Sınıf Matematik Ders Kitabı Sayfa 126. Cevapları Fersa Yayıncılık

2. 17 x 28 x 34 işlemini, çarpanları farklı şekilde gruplayıp yapınız.
Cevap:

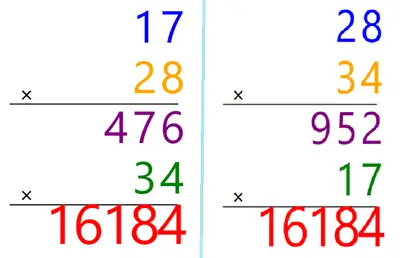
1. Yöntem: Önce ilk iki sayıyı çarpıyoruz.
(17 × 28) × 34 işleminde önce 17 ile 28’i çarpıyoruz.
17 × 28 = 476 çıkar.
Daha sonra bu sonucu 34 ile çarpıyoruz: 476 × 34 = 16 184 olur.
Yani bu yöntemle sonuç 16 184’tür.

2. Yöntem: Önce son iki sayıyı çarpıyoruz.
17 × (28 × 34) işleminde önce 28 ile 34’ü çarpıyoruz.
28 × 34 = 952 çıkar.
Sonra 17 ile 952’yi çarparız: 17 × 952 = 16 184 eder.
Bu yöntemde de sonuç değişmez.

Sonuç: Sayılar nasıl gruplanırsa gruplansın çarpım aynıdır. Sonuç yine 16 184 olur.

3. Rakamları birbirinden farklı üç basamaklı en büyük çift doğal sayı ile dört basamaklı en küçük doğal sayının zihinden çarpımı kaçtır?
Cevap: Rakamları birbirinden farklı üç basamaklı en büyük çift sayı 986’dır.
Dört basamaklı en küçük doğal sayı 1000’dir. 986 × 1000 = 986000 (1000 ile çarpmak sayıya üç sıfır eklemektir).
Sonuç: 986 000.

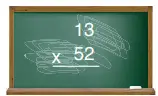
4. Bir öğrenci 13 x 52 işleminin sonucunu, çarpanların en yakın onluklarını çarparak tahmin etmiştir. Öğrencinin tahmini, işlemin sonucundan kaç eksiktir?
Cevap:
13 sayısı en yakın onluğa yuvarlandığında 10 olur.
52 sayısı en yakın onluğa yuvarlandığında 50 olur.

Öğrencinin tahmini: 10 × 50 = 500

Gerçek işlem: 13 × 52 = 676

Gerçek sonuçtan tahmini çıkarıyoruz:
676 − 500 = 176
Sonuç: 176 eksiktir.

5. Bir esnaf cuma günü dükkânında kazandığı 100 TL’lik 89 tane kâğıt parayı bankaya yatırdı. Esnafın bankaya yatırdığı para miktarı zihinden kaç TL olarak bulunur?
Cevap: Her biri 100 TL olan 89 tane banknot vardır. 100 ile çarpmak sayının sonuna iki sıfır eklemek demektir. Bu nedenle 89 × 100 = 8900 TL eder.
Sonuç: 8 900 TL.

6. Bir imalathanede 5555 bisküvi üretilmiştir. Üretilen bisküvilerden kaç tanesi ayrılırsa kalan bisküvilerle 185 paket otuzlu bisküvi paketi oluşturulabilir?
Cevap:

185 paket için gereken bisküvi sayısı:
185 × 30 = 5550

Toplam üretilen bisküvi: 5555

5555’ten 5550’si paketlerde kullanılacağı için:
5555 − 5550 = 5

Kalan 5 bisküvi pakete sığmaz.
Sonuç: 5 bisküvi ayrılmalıdır.

7. 200 000 ÷ 100 işlemi zihinden yapıldığında bölümün sonunda kaç sıfır olduğunu bulunuz.
Cevap: 200 000 ÷ 100 işleminde 100’ün iki sıfırı olduğu için sayıdan iki sıfır silinir.
200 000 → 2000 olur.

2000 sayısının sonunda 3 sıfır vardır.
Sonuç: 3.

4. Sınıf Matematik Ders Kitabı Sayfa 127. Cevapları Fersa Yayıncılık

8. Yazı tahtasında verilen işleme göre ■ + ▲ işleminin sonucu kaç bulunur?
Cevap:

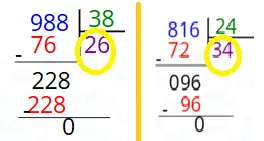
988 ÷ 38 = 26
816 ÷ 24 = 34

Tahtadaki kare (■) 26, üçgen (▲) ise 34’tür.

Bu iki sonucu topladığımızda:

26 + 34 = 60
Sonuç: 60

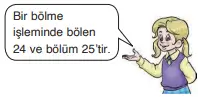
9. Cemre’nin ifadesine göre bu bölme işleminde bölünen en fazla kaçtır?
Cevap:

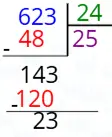
• Bölen = 24
• Bölüm = 25
• En büyük kalan = 23 (çünkü 24’ten küçük en büyük sayı)

Bölüneni hesaplayalım:
24 × 25 + 23 = 600 + 23 = 623

Görseldeki işlem de tam olarak bunu gösteriyor.

Sonuç: Bölünen en fazla 623 olur.

10. 647 ÷ 25 işleminin sonucu, bölünen en yakın onluğa yuvarlanarak tahmin ediliyor. Buna göre işlemin tahminî sonucu kaçtır?
Cevap:

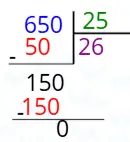
647 sayısı en yakın onluğa yuvarlandığında 650 olur.
650 ÷ 25 işlemi yapıldığında da:

• 25, 50’nin içinde 2 kere vardır.
• 25, 150’nin içinde 6 kere vardır.

Bölme işlemi 26 sonucunu verir.

Sonuç: Tahminî sonuç 26’dır.

11. Bir bölme işleminde bölüm 22, kalan 3 ve bölünen 927 ise bölen sayıyı bulunuz.
Cevap:

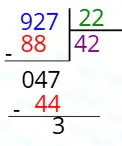
Bölünen = 927
Bölüm = 22
Kalan = 3
Bölen = ?

Adım-1: Kalanı çıkar

Bölünen = 927
Kalan = 3

927 − 3 = 924

Bu, tam bölünebilen kısmını bulmamızı sağlar.

Adım-2: Kalanı çıkarınca kalan sayı ile bölüm arasında ilişki kur

Tam bölünebilen sayı = 924
Bölüm = 22

Demek ki: Bölen × 22 = 924

Bölmek için: 924 ÷ 22 = 42
Sonuç: Bölen = 42

12. ✿ + 34 = 9 x 6
Yukarıda verilen eşitlikte ✿ yerine hangi sayı yazılmalıdır?
Cevap:

12. ✿ + 34 = 9 × 6

Önce sağ tarafı hesaplayalım:

9 × 6 = 54

Şimdi eşitlik şöyle olur:

✿ + 34 = 54

✿’ü bulmak için 34’ü çıkarırız:

54 − 34 = 20
Sonuç: 20

4. Sınıf Matematik Ders Kitabı Sayfa 128. Cevapları Fersa Yayıncılık

13. Bir lokantaya pirinç alınacaktır.

Yukarıdaki kutularda miktarları ve satış fiyatları verilen pirinçlerden hangisi alınırsa kilogramına daha az para ödeneceğini belirleyiniz.
Cevap: Hesaplayalım:

• 15 kg → 270 TL → 270 ÷ 15 = 18 TL/kg
• 18 kg → 288 TL → 288 ÷ 18 = 16 TL/kg
• 9 kg → 171 TL → 171 ÷ 9 = 19 TL/kg
• 30 kg → 510 TL → 510 ÷ 30 = 17 TL/kg

En ucuz kilogram fiyatı 16 TL/kg’dır.

Sonuç: 18 kg pirinç alınmalıdır.

14. Yukarıdaki eşitliklerde verilmeyen değerler yerine hangi sayılar yazılmalıdır? Belirleyiniz.
Cevap:

1) 124 – 24 = 🌙 × 5

Önce sol tarafı hesapla:
124 − 24 = 100

Eşitlik:
100 = 🌙 × 5

100’ü 5’e bölelim:
100 ÷ 5 = 20
🌙 = 20

2) 4 × 11 = 🙂 + 22

Sol tarafı hesapla:
4 × 11 = 44

Eşitlik:
44 = 🙂 + 22

44’ten 22 çıkar:
44 − 22 = 22
🙂 = 22

3) 450 ÷ 9 = 3 + ⭐

Önce sol tarafı hesapla:
450 ÷ 9 = 50

Eşitlik:
50 = 3 + ⭐

50’den 3 çıkar:
50 − 3 = 47
⭐ = 47

Sonuç:
🌙 = 20
🙂 = 22
⭐ = 47

15. Eylül’ün kumbarasında 12 tane 25 kuruş, Kaya’nın kumbarasında 25 tane 10 kuruş vardır. İki kardeşin paralarının eşit olması için neler yapılabilir? Açıklayınız.
Cevap:

Eylül’ün parası:
12 adet 25 kuruş
= 300 kuruş
= 3 TL

Kaya’nın parası:
25 adet 10 kuruş
= 250 kuruş
= 2,5 TL

Aralarındaki fark:
300 − 250 = 50 kuruş

Paraların EŞİT olması için iki doğru yol vardır:
1.  Eylül Kaya’ya 25 kuruş verirse

Bu, farkın yarısıdır.

Eylül: 3 TL − 0,25 TL = 2,75 TL

Kaya: 2,5 TL + 0,25 TL = 2,75 TL

İkisi de 2,75 TL olur.
Bu en doğru ve adil yöntemdir.

2. Kaya kendi parasına 50 kuruş eklerse

Eylül: 3 TL

Kaya: 2,5 TL + 0,5 TL = 3 TL

İkisi de 3 TL olur.

Kısaca:
Eylül Kaya’ya 25 kuruş verirse paraları eşit olur.
Veya Kaya kumbara­sına 50 kuruş eklerse yine eşit olur.

16. Yanda, aralarında eşitlik durumu olmayan iki matematiksel ifade verilmiştir. Bu iki ifadenin birbirine eşit olması için neler yapılabilir? Açıklayınız.
Kısa Cevap:
9 × 2 = 18 ve 25 − 5 = 20 olduğu için eşit değildir.
Eşit olmaları için 25 yerine 23 yazılırsa 23 − 5 = 18 olur.
Bu şekilde iki ifade eşit olur.

Detaylı Cevap:
İfadeyi önce hesaplayalım:

9 × 2 = 18

25 − 5 = 20

Yani: 18 ≠ 20
(İki taraf eşit değil.)

Bu iki ifadenin eşit olması için sonuçlarının aynı olması gerekir.
• 9 × 2 işleminin sonucu 18’dir.
• 25 − 5 işleminin sonucu 20’dir.

Eşitlemek için:

25 yerine 23 yazarsak:
23 − 5 = 18 olur ve iki taraf eşit olur.

Yani 25 sayısını 23 yaparsak iki ifade eşit olur.

Sonraki Ödevler

• 4. Sınıf Matematik Ders Kitabı Sayfa 122-124. Cevapları Fersa Yayınları
• 4. Sınıf Matematik Ders Kitabı Sayfa 119-121. Cevapları Fersa Yayınları
• 4. Sınıf Matematik Ders Kitabı Sayfa 114-115-116-117-118. Cevapları Fersa Yayınları
• 4. Sınıf Matematik Ders Kitabı Sayfa 109-112-113. Cevapları Fersa Yayınları