6. Sınıf Matematik Ders Kitabı Sayfa 32-33-34-35-36. Cevapları
6. Sınıf Matematik Ders Kitabı Sayfa 32-33-34-35-36. Cevapları 1. Kitap bölümünde, ders kitabı sayfa 32-33-34-35-36 konularına ait cevapları bulabilirsiniz. “Kalansız Bölünebilme Etkinlik Cevapları -2” Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 6. Sınıf Matematik Ders Kitabı Sayfa 32-33-34-35-36. Cevapları MEB Yayınları soruları dikkatlice inceleyin. Başarınızı artırın.
Kalansız Bölünebilme Etkinlik Cevapları -2
Eğer 2. Kitap (2. Dönem) cevaplarını arıyorsanız, aşağıdaki butona tıklayarak içindekiler sayfasına gidebilirsiniz.
6. Sınıf Matematik 2. Kitap Sayfaları1. Tema Sayılar ve Nicelikler (1): Doğal sayıların kalansız bölünebilme kurallarını (2, 3, 4, 5, 6, 9, 10) keşfederek, bu kuralları çeşitli problemlerde uygulama ve sayıların özellikleri analiz ediliyor.
Önceki Sayfalar: 27-28-29-30-31
İçindekiler
6. Sınıf Matematik Ders Kitabı Sayfa 32 Cevapları Birinci Kitap
Etkinlik 3
3 Ve 9 İle Kalansız Bölünebilme
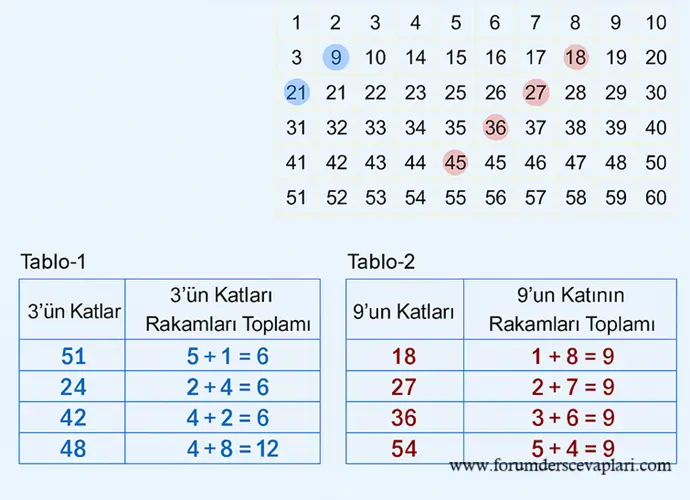
Yukarıdaki tabloda 3’ün katı olan doğal sayıları ve 9’un katı olan doğal sayıları farklı renkte kalemlerle işaretleyiniz. Daha sonra 3’ün iki basamaklı katlarından ve 9’un iki basamaklı katlarından dörder tane seçerek aşağıdaki tabloları örnekteki gibi doldurunuz.
1) Tablo-1’i inceleyerek 3’e kalansız bölünebilme ile ilgili bir genelleme yapabilir misiniz? Yaptığınız genellemeyi yazınız ve arkadaşlarınızla paylaşınız.
Cevap: Bir sayının 3’e bölünüp bölünmediğini anlamak için sayının rakamlarını toplarız. Eğer bu toplam 3’e kalansız bölünüyorsa, o sayı da 3’e kalansız bölünür.
Örneğin: 123 sayısının rakamları toplamı 1+2+3=6’dır. 6 sayısı 3’e bölünebildiği için 123 de 3’e bölünebilir.
2) Tablo-2’yi inceleyerek 9’a kalansız bölünebilme ile ilgili bir genelleme yapabilir misiniz? Yaptığınız genellemeyi yazınız ve arkadaşlarınızla paylaşınız.
Cevap: Bir sayının 9’a bölünüp bölünmediğini anlamak için de aynı yöntemi kullanırız. Sayının rakamlarını toplarız. Eğer bu toplam 9’a bölünebiliyorsa, sayı da 9’a bölünür.
Örneğin: 234 sayısının rakamları toplamı 2+3+4=9’dur. 9 sayısı 9’a bölünebildiği için 234 de 9’a bölünebilir.
3) Farklı sayılar kullanarak yaptığınız genellemelerin yönteminizi karşılayıp karşılamadığını kontrol ediniz.
Cevap: Farklı örnek sayılar seçerek kuralımızı kontrol edebiliriz. Önce rakamlarını toplarız, sonra bu toplamın 3’e veya 9’a bölünüp bölünmediğine bakarız.
135 sayısı → 1+3+5=9. 9 hem 3’e hem de 9’a bölünebildiği için 135 sayısı da hem 3’e hem 9’a bölünür.
218 sayısı → 2+1+8=11. 11 ne 3’e ne de 9’a bölünemez. Bu yüzden 218 sayısı da bölünmez.
Bu şekilde farklı sayılar deneyerek yaptığımız genellemeyi doğrulamış oluruz.
4) Bir sayının 3 ile kalansız bölünebilmesi için sağlaması gereken kriterler nelerdir?
Cevap: Bir sayının rakamları toplamı 3’e bölünebiliyorsa, o sayı 3 ile kalansız bölünebilir.
Örneğin: 456 sayısı → 4+5+6=15. 15 sayısı 3’e bölünebildiği için 456 da 3’e bölünür.
5) Bir sayının 9 ile kalansız bölünebilmesi için sağlaması gereken kriterler nelerdir?
Cevap: Bir sayının rakamları toplamı 9’a bölünebiliyorsa, o sayı 9 ile kalansız bölünebilir.
Örneğin: 729 sayısı → 7+2+9=18. 18 sayısı 9’a bölünebildiği için 729 da 9’a bölünür.
İhtiyacınız olan içeriğe aşağıdaki ana kaynaklardan ulaşabilirsiniz:
6. Sınıf Matematik Ders Kitabı Sayfa 33 Cevapları Birinci Kitap
Örnek 4
Aşağıdaki doğal sayılardan 3 ile kalansız bölünebilenleri işaretleyiniz.
Cevap: Bir sayının rakamları toplamı 3’e bölünebiliyorsa, o sayı 3 ile kalansız bölünür.
27 → 2+7=9 → 9, 3’e bölünür ✔
152 → 1+5+2=8 → 8, 3’e bölünmez ✘
3600 → 3+6+0+0=9 → 9, 3’e bölünür ✔
305 → 3+0+5=8 → 8, 3’e bölünmez ✘
2045 → 2+0+4+5=11 → 11, 3’e bölünmez ✘
249 → 2+4+9=15 → 15, 3’e bölünür ✔
5314 → 5+3+1+4=13 → 13, 3’e bölünmez ✘
1002 → 1+0+0+2=3 → 3, 3’e bölünür ✔
✅ 3 ile bölünebilen sayılar: 27, 3600, 249, 1002
Örnek 5
Aşağıdaki doğal sayılardan 9 ile kalansız bölünebilenleri işaretleyiniz.
Cevap: Bir sayının rakamları toplamı 9’a bölünebiliyorsa, o sayı 9 ile kalansız bölünür.
45 → 4+5=9 → 9, 9’a bölünür ✔
184 → 1+8+4=13 → 13, 9’a bölünmez ✘
314 → 3+1+4=8 → 8, 9’a bölünmez ✘
6016 → 6+0+1+6=13 → 13, 9’a bölünmez ✘
3222 → 3+2+2+2=9 → 9, 9’a bölünür ✔
873 → 8+7+3=18 → 18, 9’a bölünür ✔
3647 → 3+6+4+7=20 → 20, 9’a bölünmez ✘
7992 → 7+9+9+2=27 → 27, 9’a bölünür ✔
✅ 9 ile bölünebilen sayılar: 45, 3222, 873, 7992
Örnek 6
▲ve ▇ birer doğal sayıyı temsil etmektedir.
14▲ üç basamaklı doğal sayısı 3 ile kalansız bölünebilmektedir. 27▇ üç basamaklı doğal sayısı 9 ile kalansız bölünebilmektedir.
Buna göre ▲+ ▇’nin alabileceği en büyük değer kaçtır?
Cevap: ▲ ve ▇ birer doğal sayıyı temsil etmektedir.
14▲ üç basamaklı doğal sayısı 3 ile kalansız bölünebiliyor.
Rakamlar toplamı: 1+4+▲ = 5+▲.
Bu toplamın 3’e bölünebilmesi için ▲=1, 4, 7 olabilir. En büyük değer: 7.
27▇ üç basamaklı doğal sayısı 9 ile kalansız bölünebiliyor.
Rakamlar toplamı: 2+7+▇ = 9+▇.
Bu toplamın 9’a bölünebilmesi için ▇=0 veya 9 olabilir. En büyük değer: 9.
Sonuç: ▲+▇ = 7+9 = 16
Çünkü: ▲=7 seçildiğinde 147 sayısı 3’e bölünür, ▇=9 seçildiğinde 279 sayısı 9’a bölünür. Bu durumda ▲+▇ en büyük değeri 16 olur.
6. Sınıf Matematik Ders Kitabı Sayfa 34 Cevapları Birinci Kitap
Etkinlik 4
Hem 2’ye Hem De 3’e Kalansız Bölünebilme
Yandaki tabloda 2’nin katlarını ve 3’ün katlarını farklı renkte kalemlerle işaretleyiniz.
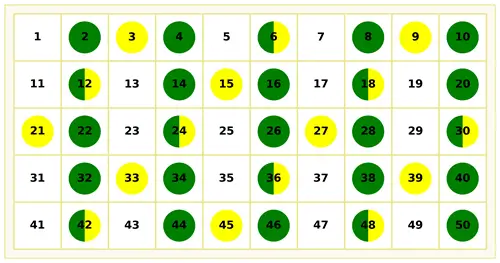
Buna göre aşağıdaki soruları cevaplayınız.
1) İki farklı renkte kalemle işaretlediğiniz sayıları sırasıyla yazınız. Bu sayıların hangi sayının katı olduğunu belirleyiniz
Cevap: 1) İki farklı renkte işaretlenen sayılar ve hangi sayının katı oldukları:
2’nin katları: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50 → 2’nin katı
3’ün katları: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48 → 3’ün katı
2) Hem 2’ye hem de 3’e kalansız bölünebilen sayılarla ilgili bir genelleme yapabilir misiniz? Yaptığınız genellemeyi yazınız ve arkadaşlarınızla paylaşınız.
Cevap: Hem 2’nin hem 3’ün katı olan sayılar aynı zamanda 6’nın katlarıdır.
3) Farklı sayılar kullanarak yaptığınız genellemelerin yönteminizi karşılayıp karşılamadığını kontrol ediniz.
Cevap: Mesela 4 ve 5 sayısını seçelim:
4 ve 5’in katı olan sayılar aynı zamanda 20’nin katı olur.
Bu da gösteriyor ki genellememiz doğru.
4) Bir sayının hem 2’ye hem de 3’e kalansız bölünebilmesi için sağlaması gereken kriterler nelerdir?
Cevap: Sayı çift olmalı (2’ye bölünebilmesi için).
Rakamları toplamı 3’e bölünebilmeli (3’e bölünebilmesi için).
Yani sayı bu iki şartı sağlarsa 6’ya da tam bölünür.
Örnek 7
Aşağıdaki doğal sayılardan 6 ile kalansız bölünebilenleri işaretleyiniz.
Cevap: Bir sayı 6’ya bölünebilmek için hem 2’ye hem de 3’e bölünebilmelidir.
755 → Tek sayı, 2’ye bölünmez ✘
564 → Çift, rakamları toplamı 5+6+4=15, 3’e bölünür ✔
1024 → Çift ama 1+0+2+4=7, 3’e bölünmez ✘
82 → Çift ama 8+2=10, 3’e bölünmez ✘
1251 → Tek sayı ✘
54 → Çift, 5+4=9, 3’e bölünür ✔
2000 → Çift ama 2+0+0+0=2, 3’e bölünmez ✘
906 → Çift, 9+0+6=15, 3’e bölünür ✔
✅ 6’ya bölünebilen sayılar: 564, 54, 906
6. Sınıf Matematik Ders Kitabı Sayfa 35 Cevapları Birinci Kitap
Etkinlik 5
4 İle Kalansız Bölünebilme
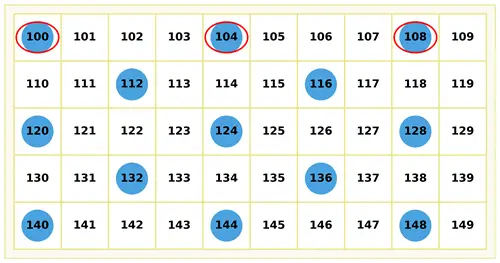
Tabloda verilen sayılardan 4’ün katı olan ilk üç sayı işaretlenmiştir. Örüntüden yola çıkarak 4’ün katı olan diğer doğal sayıları işaretleyiniz.
1) Bu sayıları sırasıyla yazarak 4’e kalansız bölünebilme ile ilgili bir genelleme yapabilir misiniz? Yaptığınız genellemeyi yazınız ve arkadaşlarınızla paylaşınız.
Cevap: Bir sayının son iki rakamına bakarsak, bu iki rakamdan oluşan sayı 4’e bölünüyorsa bütün sayı da 4’e tam bölünür.
Örnek:
316 → son iki rakam 16, 16 ÷ 4 = 4 → 316 da 4’e tam bölünür.
123 → son iki rakam 23, 23 ÷ 4 = 5 kalan 3 → 123, 4’e tam bölünmez.
2) Farklı sayılar kullanarak yaptığınız genellemelerin yönteminizi karşılayıp karşılamadığını kontrol ediniz.
Cevap: 68 → son iki rakam 68, 68 ÷ 4 = 17 → bölünür.
202 → son iki rakam 02, 2 ÷ 4 olmaz → bölünmez.
740 → son iki rakam 40, 40 ÷ 4 = 10 → bölünür.
Bu örnekler, kuralın her sayıda işe yaradığını gösteriyor.
3) Bir sayının 4 ile kalansız bölünebilmesi için sağlaması gereken kriterler nelerdir?
Cevap: Bir sayının 4 ile kalansız bölünebilmesi için şunu yapmak gerekir.
Sadece en sondaki iki rakama bakalım. Bu iki rakamdan oluşan sayı 4’ün çarpımı ise, bütün sayı da 4’e tam bölünür.
Örneğin 316 sayısında son iki rakam 16’dır.
16, 4 x 4 = 16 olduğu için 316 da 4’e tam bölünür.
523 sayısında son iki rakam 23.
23, 4’ün hiçbir katı değildir. Bu yüzden 523, 4’e tam bölünmez.
Yani büyük sayının tamamını kontrol etmeye gerek yok, yalnızca son iki rakama bakmak yeterli.
Örnek 8
Aşağıdaki doğal sayılardan 4 ile kalansız bölünebilenleri işaretleyiniz.
Cevap: Son iki rakama bak; bu iki rakam 4’ün katıysa, sayı 4’e tam bölünür.
64 → son iki rakam 64 → 64 ÷ 4 = 16 ✔
350 → son iki rakam 50 → 50 ÷ 4 = 12 kalan 2 ✖
128 → son iki rakam 28 → 28 ÷ 4 = 7 ✔
1074 → son iki rakam 74 → 74 ÷ 4 = 18 kalan 2 ✖
3142 → son iki rakam 42 → 42 ÷ 4 = 10 kalan 2 ✖
784 → son iki rakam 84 → 84 ÷ 4 = 21 ✔
5056 → son iki rakam 56 → 56 ÷ 4 = 14 ✔
870 → son iki rakam 70 → 70 ÷ 4 = 17 kalan 2 ✖
✅ 4’e tam bölünenler: 64, 128, 784, 5056
Örnek 9
Yandaki dijital saatte, saati ve dakikayı gösteren sayılar yan yana yazılarak dört basamaklı 1009 doğal sayısı elde edilmiştir.
Benzer şekilde elde edilecek doğal sayının hem 5’e hem de 9’a kalansız bölünebilmesi için en az kaç dakikanın geçmesi gerektiğini bulunuz.
Cevap: Saat ve dakikayı yan yana yazarak dört basamaklı sayı yapıyoruz.
10:09’dan başlayacağız. Hem 5’e hem 9’a bölünebilecek ilk sayıyı arıyoruz.
5’e bölünmesi için: Sayının son rakamı 0 ya da 5 olmalı.
9’a bölünmesi için: Rakamların toplamı 9’un katı olmalı.
Dakikaları arttıralım:
10:10 → 1010 → son rakam 0 ✔ ama 1+0+1+0=2 ✖
10:15 → 1015 → son rakam 5 ✔ ama 1+0+1+5=7 ✖
10:20 → 1020 → 1+0+2+0=3 ✖
10:25 → 1025 → 1+0+2+5=8 ✖
10:30 → 1030 → 1+0+3+0=4 ✖
10:35 → 1035 → son rakam 5 ✔ ve 1+0+3+5=9 ✔
İşte bulduk: 1035 hem 5’e hem 9’a bölünür.
10:09’dan 10:35’e kadar geçen süre: 26 dakika
6. Sınıf Matematik Ders Kitabı Sayfa 36 Cevapları Birinci Kitap
Problem 1
Yusuf, Ayşe, Ali ve Ceren “Aklımdan bir sayı tuttum, bil bakalım!” oyununu oynamaktadırlar. Bu oyunda aklından bir sayı tutan kişi, ipuçları vererek arkadaşlarının sayıyı bulmasını beklemektedir.
Akıllarından tuttukları doğal sayılar ile ilgili ipuçları aşağıda verilmiştir.

Yusuf’un sayısı 738,
Ayşe’nin sayısı 95,
Ceren’in sayısı 98
Ali’nin sayısı 108’dir.
Buna göre aşağıdaki soruları cevaplayınız.
a) Yusuf ve Ali’nin akıllarından tuttukları sayıların farkının 9 ile kalansız bölünüp bölünemeyeceğini belirleyiniz.
Cevap: Evet, fark 9 ile kalansız bölünür.
Yusuf ve Ali’nin farkı:
738 − 108 = 630.
9 ile bölünebilme kuralı: rakamların toplamı 9’un katıysa sayı 9’a tam bölünür.
6 + 3 + 0 = 9, yani 630 9’a tam bölünür.
b) Ceren ve Ayşe’nin akıllarından tuttukları sayıların toplamının 6 ile kalansız bölünüp bölünemeyeceğini belirleyiniz.
Cevap: Hayır, toplam 6 ile kalansız bölünmez.
Ceren ve Ayşe’nin toplamı: 98 + 95 = 193.
6 ile bölünebilmesi için hem 2’ye (çift olması) hem 3’e bölünmesi gerekir. 193 tek bir sayı (son rakam 3) olduğundan 2’ye bölünmez → 6’ya bölünmez.
c) Ceren, Ayşe ve Yusuf’un akıllarından tuttukları sayıların toplamının 10 ile bölümünden kalan sayıyı belirleyiniz.
Cevap: Kalan 1.
Ceren + Ayşe + Yusuf = 98 + 95 + 738 = 931.
10 ile bölümünden kalan, sayının son basamağıdır. 931’in son basamağı 1.
ç) Bölme işlemi yapmadan kalansız bölünebilme kriterlerinin problemin çözümünde sağladığı kullanışlılığını değerlendiriniz.
Cevap: Bölünebilme kuralları çok kullanışlıdır çünkü bölme işlemine gerek kalmadan kısa yoldan karar veririz:
2 için → son rakam çift mi?
3 için → rakamların toplamı 3’ün katı mı?
4 için → son iki rakam 4’e bölünüyor mu?
9 için → rakamların toplamı 9’un katı mı?
10 için → son rakam 0 mı?
Bunları kullanarak yukarıdaki soruları hızlıca ve kolayca çözdük — uzun bölme yapmaya gerek kalmadı.
6. Sınıf Matematik Ders Kitabı Sayfa 37 Cevapları Birinci Kitap
İzleme Testi
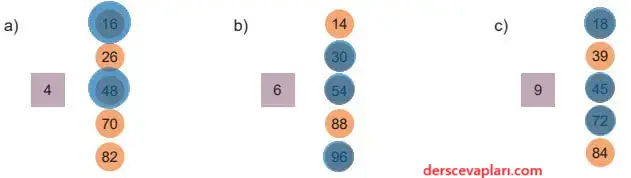
1) Aşağıda karelerin içindeki sayıya kalansız bölünebilecek doğal sayıları işaretleyiniz.
Cevap: Karelerin içindeki sayıya kalansız bölünebilecek doğal sayılar.
a) (4) → 16, 48
b) (6) → 30, 54, 96
c) (9) → 18, 45, 72
2) Aşağıdaki ifadelerden doğru olanların başına “D”, yanlış olanların başına “Y” yazınız.
Cevap:
a) __Y__ Bir doğal sayının birler basamağı 0, 2, 4, 6 veya 8 ise o sayı 6 ile kalansız bölünür.
b) __D__ Bir doğal sayının rakamlarının toplamı 9’un katı ise o sayı 3 ile kalansız bölünür.
c) __D__ Hem 2’ye hem 5’e kalansız bölünen doğal sayılar 10 ile de kalansız bölünür.
ç) __D__ Bir doğal sayının son iki basamağı 00 veya 4’ün katı ise o sayı 4 ile kalansız bölünür.
d) __Y__ Bir doğal sayının birler basamağı 0 veya 9 ise o sayı 9 ile kalansız bölünür.
3) Şermin, istediği bir hikâye kitabını almak için harçlıklarından biriktirdiği 175 TL ile kitapçıya gitmiştir. Alacağı hikâye kitabının fiyatı TL cinsinden hem 2 ile hem de 3 ile kalansız bölünebilen bir doğal sayıdır.
Şermin, biriktirdiği para ile istediği hikâye kitabını alabildiğine göre bu hikâye kitabının fiyatının en fazla kaç TL olabileceğini bulunuz.
Cevap: Şermin 175 TL ile alabileceği en büyük kitap fiyatı; fiyat hem 2’ye hem 3’e bölünmeli → yani 6’nın katı olmalı.
175’in altındaki en büyük 6’nın katı = 174 TL.
Cevap: 174 TL
4) Üzerinde doğal sayılar bulunan balonlar aşağıda verilmiştir.

Oğuzhan, attığı oklarla üzerinde hem 5 hem de 9 ile kalansız bölünebilen doğal sayıların yazılı olduğu balonları patlatmıştır.
Buna göre hangi renk balonların patlamadığını bulunuz.
Cevap: Hem 5’e hem 9’a bölünebilmesi için 45’in katı olması gerekir. 45’in katı olanlar: 180, 270, 495.
Böylece patlamayan balonlar = 335 (kırmızı) ve 594 (sarı).
Cevap: Kırmızı ve sarı balonlar patlamadı.
Önceki Sayfalar: 27-28-29-30-31